已知函數f(ax)=x,g(x)=2loga(2x+t-2),其中a>0且a≠1,t∈R.
(1)求函數y=f(x)的解析式,并指出其定義域;
(2)若t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2,求實數a的值;
(3)已知0<a<1,當x∈[1,2]時,有f(x)≥g(x)恒成立,求實數t的取值范圍.
【答案】
分析:(1)求函數y=f(x)的解析式,可以用換元法求解;
(2)根據函數的性質判斷出函數的最小值,令其等于2,利用此方程求出實數a的值;
(3)令F(x)=g(x)-f(x),求出其在x∈[1,2]時最大值,讓最大值小于等于0即可得到實數t的不等式,解此不等式即可.
解答:解:(1)令m=a
x,則x=log
am,則y=f(x)=log
ax,定義域為(0,+∞);
(2)由題F(x)=g(x)-f(x)=2log
a(2x+2)-log
ax=log
a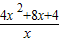
=og
a(
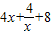
),
∵
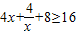
,等號當且僅當
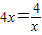
,即當x=1時成立
又F(x)=g(x)-f(x)有最小值2,可得log
a16=2
故a
2=16,a=4
(3)f(x)≥g(x),可得log
ax≥2log
a(2x+t-2),
又0<a<1,可得
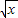
≤2x+t-2,可得t≥
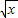
-2x+2=-
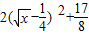
由0<a<1,當x∈[1,2]時,有f(x)≥g(x)恒成立可得
t≥
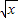
-2x+2=-
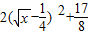
在x∈[1,2]恒成立
由于x=1時-
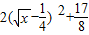
取到最大值1
可得t≥1
點評:本題考查函數的恒成立的問題,函數恒成立問題的求解,關鍵正確轉化,通過過轉化為其等價的方程或不等式解決恒成立的問題中的參數的范圍,是此類題的固定思路.本題抽象難以理解.

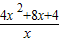 =oga(
=oga(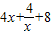 ),
),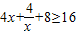 ,等號當且僅當
,等號當且僅當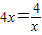 ,即當x=1時成立
,即當x=1時成立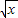 ≤2x+t-2,可得t≥
≤2x+t-2,可得t≥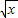 -2x+2=-
-2x+2=-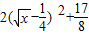
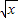 -2x+2=-
-2x+2=-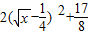 在x∈[1,2]恒成立
在x∈[1,2]恒成立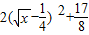 取到最大值1
取到最大值1
