將兩粒均勻的骰子各拋擲一次,觀察向上的點數,計算:
(1)共有多少種不同的結果?并試著列舉出來.
(2)兩粒骰子點數之和等于3的倍數的概率;
(3)兩粒骰子點數之和為4或5的概率.
【答案】
分析:(1)每一粒均勻的骰子拋擲一次,都有6種結果,根據分步計數原理,求得將兩粒均勻的骰子各拋擲一次得到不同結果的個數.
(2)用列舉法求得兩粒骰子點數之和等于3的倍數的有12種,由此可得兩粒骰子點數之和等于3的倍數的概率.
(3)用列舉法求得兩粒骰子點數之和為4或5的有7種,由此可得兩粒骰子點數之和為4或5的概率.
解答:解:(1)每一粒均勻的骰子拋擲一次,都有6種結果,根據分步計數原理,所有可能結果共有6×6=36種. …(4分)
(2)兩粒骰子點數之和等于3的倍數的有以下12種:(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),
(3,6),(6,3),(5,4),(4,5),(6,6),共有12個結果,
因此,兩粒骰子點數之和等于3的倍數的概率是
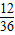
=

. …(8分)
(3)兩粒骰子點數之和為4或5的有以下7種:(2,2),(1,3),(3,1),(2,3),(3,2),(1,4),(4,1),
因此,兩粒骰子點數之和為4或5的概率為
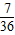
. …(12分)
點評:本題考查古典概型問題,可以列舉出試驗發生包含的事件和滿足條件的事件,應用列舉法來解題是這一部分的最主要思想,屬于基礎題.

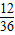 =
= . …(8分)
. …(8分)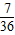 . …(12分)
. …(12分)

 閱讀快車系列答案
閱讀快車系列答案