
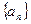 中,前n項和
中,前n項和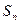 滿足:
滿足: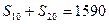 ,
,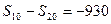 。
。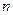 和
和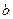 值:
值: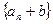 中的連續(xù)三項,其中
中的連續(xù)三項,其中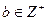 ;
; 小學課時作業(yè)全通練案系列答案
小學課時作業(yè)全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案科目:高中數(shù)學 來源:不詳 題型:填空題
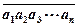 為一個
為一個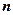 位正整數(shù),其中
位正整數(shù),其中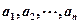 都是正整數(shù),
都是正整數(shù), .若對任意的正整數(shù)
.若對任意的正整數(shù)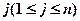 ,
, 至少存在另一個正整數(shù)
至少存在另一個正整數(shù)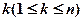 ,使得
,使得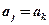 ,則稱這個數(shù)為“
,則稱這個數(shù)為“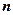 位重復數(shù)”.根據(jù)上述定義,“四位重復數(shù)”的個數(shù)為.____________.
位重復數(shù)”.根據(jù)上述定義,“四位重復數(shù)”的個數(shù)為.____________. 查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 n項的乘積等于Tn=
n項的乘積等于Tn=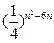 (n∈N*),
(n∈N*),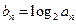 ,則
,則
| A.S6 | B.S5 | C.S4 | D.S3 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.6 | B.8 | C.10 | D.12 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com