已知定義域為[0,1]的函數同時滿足以下三個條件:①對任意x∈[0,1],總有f(x)≥0;②f(1)=1;③若x1≥0,x2≥0,x1+x2≤1,則有f(x1+x2)≥f(x1)+f(x2)成立.
(1)求f(0)的值;
(2)函數g(x)=2x-1在區間[0,1]上是否同時適合①②③?并予以證明;
(3)假定存在x0∈[0,1],使得f(x0)∈[0,1],且f(f(x0))=x0,求證:f(x0)=x0.
解:(1)由①知:f(0)≥0;由③知:f(0+0)≥f(0)+f(0),即f(0)≤0;
∴f(0)=0
(2 ) 證明:由題設知:g(1)=2-1=1;
由x∈[0,1]知2
x∈[1,2],得g(x)∈[0,1],有g(x)≥0;
設x
1≥0,x
2≥0,x
1+x
2≤1,則
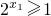
,
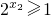
;
∴
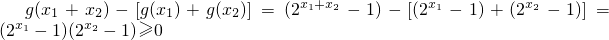
即g(x
1+x
2)≥g(x
1)+g(x
2)
∴函數g(x)=2
x-1在區間[0,1]上同時適合①②③.
(3)證明:若f(x
0)>x
0,則由題設知:f(x
0)-x
0∈[0,1],且由①知f[f(x
0)-x
0]≥0,
∴由題設及③知:x
0=f(f(x
0))=f[(f(x
0)-x
0)+x
0]=f[f(x
0)-x
0]+f(x
0)≥f(x
0)
矛盾;
若f(x
0)<x
0,則則由題設知:x
0-f(x
0)∈[0,1],且由①知f[x
0-f(x
0)]≥0,
∴同理得:f(x
0)=f[(x
0-f(x
0))+f(x
0)]=f[x
0-f(x
0)]+f(f(x
0))≥f(f(x
0))=x
0,矛盾;
故由上述知:f(x
0)=x
0.
分析:(1)由①知:f(0)≥0;由③知f(0)≤0,從而得到f(0)=0.
(2)由題設知g(1)=1;由x∈[0,1]知2
x∈[1,2],得g(x)∈[0,1],有g(x)≥0;設x
1≥0,x
2≥0,x
1+x
2≤1,則
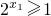
,
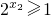
;由此能夠證明函數g(x)=2
x-1在區間[0,1]上同時適合①②③.
(3)若f(x
0)>x
0,則由題設知f(x
0)-x
0∈[0,1],且由①知f[f(x
0)-x
0]≥0,由此入手能證明f(x
0)=x
0.
點評:本題考查函數值的求法和函數恒成立問題的應用,解題時要認真審題,仔細解答.

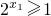 ,
,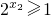 ;
;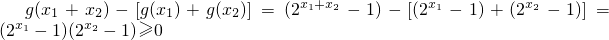
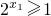 ,
,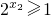 ;由此能夠證明函數g(x)=2x-1在區間[0,1]上同時適合①②③.
;由此能夠證明函數g(x)=2x-1在區間[0,1]上同時適合①②③.

 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案