
設滿足以下兩個條件的有窮數列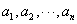 為
為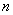
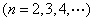 階“期待數列”:
階“期待數列”:
①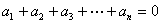 ;②
;②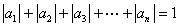 .
.
(1)若等比數列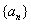 為
為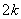 (
(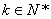 )階“期待數列”,求公比
)階“期待數列”,求公比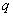 ;
;
(2)若一個等差數列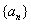 既是
既是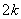 (
(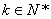 )階“期待數列”又是遞增數列,求該數列的通項公式;
)階“期待數列”又是遞增數列,求該數列的通項公式;
(3)記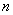 階“期待數列”
階“期待數列”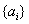 的前
的前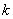 項和為
項和為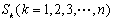 :
:
(ⅰ)求證: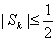 ;
;
(ⅱ)若存在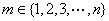 使
使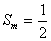 ,試問數列
,試問數列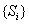 能否為
能否為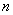 階“期待數列”?若能,求出所有這樣的數列;若不能,請說明理由.
階“期待數列”?若能,求出所有這樣的數列;若不能,請說明理由.
(1)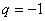 .(2)
.(2)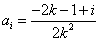 .(3)(ⅰ)利用前n項和進行放縮證明.(ⅱ)數列
.(3)(ⅰ)利用前n項和進行放縮證明.(ⅱ)數列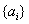 和數列
和數列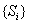
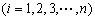 不能為
不能為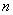 階“期待數列”.
階“期待數列”.
【解析】
試題分析:(1)若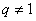 ,則由①
,則由①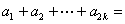
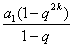 =0,得
=0,得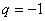 ,
,
由②得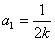 或
或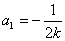 .
.
若 ,由①得,
,由①得,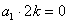 ,得
,得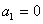 ,不可能.
,不可能.
綜上所述,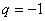 .
.
(2)設等差數列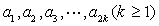 的公差為
的公差為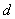 ,
,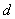 >0.
>0.
∵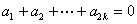 ,∴
,∴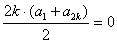 ,
,
∴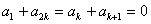 ,
,
∵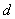 >0,由
>0,由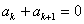 得
得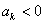 ,
,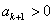 ,
,
由題中的①、②得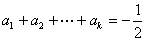 ,
,
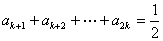 ,
,
兩式相減得,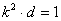 , ∴
, ∴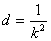 ,
,
又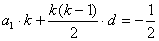 ,得
,得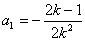 ,
,
∴ .
.
(3)記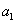 ,
,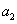 ,…,
,…,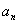 中非負項和為
中非負項和為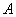 ,負項和為
,負項和為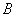 ,
,
則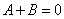 ,
,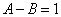 ,得
,得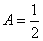 ,
,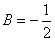 ,
,
(ⅰ)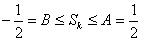 ,即
,即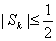 .
.
(ⅱ)若存在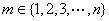 使
使 ,由前面的證明過程知:
,由前面的證明過程知:
 ,
,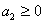 ,…,
,…,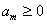 ,
,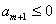 ,
,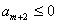 ,…,
,…, ,
,
且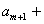
 …
…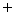
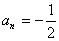 .
.
記數列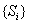
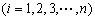 的前
的前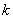 項和為
項和為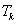 ,
,
則由(ⅰ)知,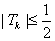 ,
,
∴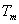 =
=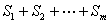
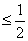 ,而
,而 ,
,
∴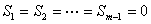 ,從而
,從而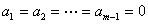 ,
,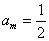 ,
,
又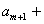
 …
…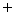
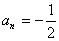 ,
,
則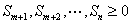 ,
,
∴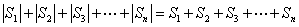 ,
,
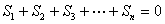 與
與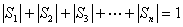 不能同時成立,
不能同時成立,
所以,對于有窮數列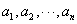
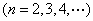 ,若存在
,若存在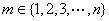 使
使 ,則數列
,則數列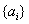 和數列
和數列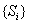
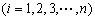 不能為
不能為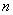 階“期待數列”.
階“期待數列”.
考點:本題考查了數列的通項公式及前n項和
點評:數列的通項公式及應用是數列的重點內容,數列的大題對邏輯推理能力有較高的要求,在數列中突出考查學生的理性思維,這是近幾年新課標高考對數列考查的一個亮點,也是一種趨勢


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| n |
 |
| i=1 |
| ai |
| i |
| 1 |
| 2 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省安慶市望江二中高三(上)第一次月考數學試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com