提分百分百檢測卷單元期末測試卷系列答案科目：高中數學 來源：2010-2011年浙江省高二下學期第二次階段性考試文數 題型：選擇題
給定函數①
，②
，③
，④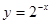
，其中在區間[0，+
）上單調遞
減的函數序號是 （ ）
A.②④ B.②③ C.③④ D.①④
查看答案和解析>>
科目：高中數學 來源：2012年全國普通高等學校招生統一考試理科數學（北京卷解析版） 題型：解答題
已知函數
，（
），
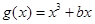
（1）若曲線
與曲線
在它們的交點（1，c）處具有公共切線，求a,b的值
（2）當
時，若函數
的單調區間，并求其在區間（-∞，-1）上的最大值。
【解析】（1）
，
∵曲線與曲線在它們的交點（1，c）處具有公共切線
∴
，
∴
（2）令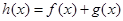
，當
時，
令
，得
時，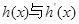
的情況如下：
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函數
的單調遞增區間為
，
，單調遞減區間為
當
，即
時，函數在區間
上單調遞增，在區間上的最大值為
，
當
且
，即
時，函數在區間內單調遞增，在區間
上單調遞減，在區間上的最大值為
當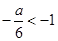
，即a>6時，函數在區間內單調遞贈，在區間內單調遞減，在區間
上單調遞增。又因為
所以在區間上的最大值為。
查看答案和解析>>
科目：高中數學 來源： 題型：
（本小題滿分15分）
已知函數
。
⑴求函數
的最小值，并求取得最小值時
的值；
⑵將得圖象向右平移
個單位后得到函數
的圖象，使得在區間
上單調遞
增，寫出一個滿足條件的函數的解析式。
查看答案和解析>>
科目：高中數學 來源： 題型：
（本小題滿分15分）
已知函數
。
⑴求函數
的最小值，并求取得最小值時
的值；
⑵將得圖象向右平移
個單位后得到函數
的圖象，使得在區間
上單調遞
增，寫出一個滿足條件的函數的解析式。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，在區間
上單調遞增，則實數
的取值范圍為 ▲ ．
(ω>0)在區間
上單調遞 增，在區間
上單調遞減，則
( )
B．
C． 2 D．3