
【題目】如圖,扇形![]() 的半徑為
的半徑為![]() ,圓心角
,圓心角![]() ,點
,點![]() 為弧
為弧![]() 上一點,
上一點,![]() 平面
平面![]() 且
且![]() ,點
,點![]() 且
且![]() ,
,![]() ∥平面
∥平面![]() .
.
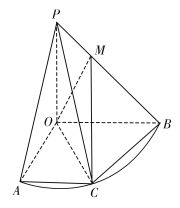
(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成二面角的正弦值的大小.
所成二面角的正弦值的大小.
【答案】(1)見證明;(2) ![]()
【解析】
(1)如圖,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,結合
,結合![]() ∥平面
∥平面![]() ,得到
,得到![]() ∥
∥![]() ,從而求得
,從而求得![]() ,根據余弦定理得
,根據余弦定理得![]() ,得到
,得到![]() ,得到
,得到![]() ,因為
,因為![]() 平面
平面![]() ,所以
,所以![]() ,得到
,得到![]() 平面
平面![]() ,再利用面面垂直的判定定理證得平面
,再利用面面垂直的判定定理證得平面![]()
![]() 平面
平面![]() ;
;
(2)由(1)的條件,得到![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() ,得到點的坐標,求得面的法向量,用法向量所成角的余弦值得到二面角的余弦值,再應用同角三角函數關系式求得其正弦值,得到答案.
,得到點的坐標,求得面的法向量,用法向量所成角的余弦值得到二面角的余弦值,再應用同角三角函數關系式求得其正弦值,得到答案.
(1)如圖,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
![]()
![]() ∥平面
∥平面![]() ,
,![]()
![]() ∥
∥![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 在
在![]() 中,根據余弦定理得
中,根據余弦定理得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
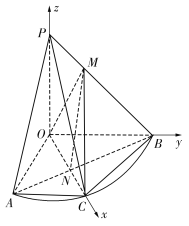
(2)由(1)得![]() ,如圖建立空間直角坐標系
,如圖建立空間直角坐標系![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 點
點![]() 且
且![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則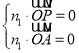 ,即
,即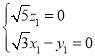 ,
,
令![]() ,得
,得![]() ,
,![]() ,
,![]()
![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則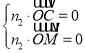 ,即
,即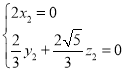 ,即
,即 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,![]()
![]() ,
,
設平面![]() 和平面
和平面![]() 所成二面角的大小為
所成二面角的大小為![]() ,
,
則![]() ,
,![]() ,
,
∴平面![]() 和平面
和平面![]() 所成二面角的正弦值的大小為
所成二面角的正弦值的大小為![]()


科目:高中數學 來源: 題型:
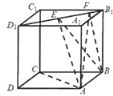
【題目】如圖,正方形![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() .
.![]() ,且
,且![]() ,則下列結論中錯誤的是( )
,則下列結論中錯誤的是( )
A.![]() ;
;
B.三棱錐![]() 體積是定值;
體積是定值;
C.二面角![]() 的平面角大小是定值;
的平面角大小是定值;
D.![]() 與平面
與平面![]() 所成角等于
所成角等于![]() 與平面
與平面![]() 所成角;
所成角;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“辛卜生公式”給出了求幾何體體積的一種計算方法:夾在兩個平行平面之間的幾何體,如果被平行于這兩個平面的任何平面所截,截得的截面面積是截面高(不超過三次)的多項式函數,那么這個幾何體的體積,就等于其上底面積、下底面積與四倍中截面面積的和乘以高的六分之一.即:![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
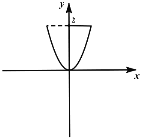
,![]() 依次為幾何體的高,下底面積,上底面積,中截面面積.如圖,現將曲線
依次為幾何體的高,下底面積,上底面積,中截面面積.如圖,現將曲線![]() 與直線
與直線![]() 及
及![]() 軸圍成的封閉圖形繞
軸圍成的封閉圖形繞![]() 軸旋轉一周得到一個幾何體.利用辛卜生公式可求得該幾何體的體積
軸旋轉一周得到一個幾何體.利用辛卜生公式可求得該幾何體的體積![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 是線段
是線段![]() 上的一個動點.
上的一個動點.
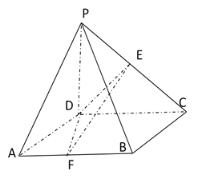
(Ⅰ)求證:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)當點![]() 是線段
是線段![]() 上的中點時,求二面角
上的中點時,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正整數數列![]() 滿足
滿足![]() (p,q為常數),其中
(p,q為常數),其中![]() 為數列
為數列![]() 的前n項和.
的前n項和.
(1)若![]() ,
,![]() ,求證:
,求證:![]() 是等差數列;
是等差數列;
(2)若數列![]() 為等差數列,求p的值;
為等差數列,求p的值;
(3)證明:![]() 的充要條件是
的充要條件是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有限個元素組成的集合為![]() ,
,![]() ,集合
,集合![]() 中的元素個數記為
中的元素個數記為![]() ,定義
,定義![]() ,集合
,集合![]() 的個數記為
的個數記為![]() ,當
,當![]() ,稱集合
,稱集合![]() 具有性質
具有性質![]() .
.
(1)設集合![]() 具有性質
具有性質![]() ,判斷集合
,判斷集合![]() 中的三個元素是否能組成等差數列,請說明理由;
中的三個元素是否能組成等差數列,請說明理由;
(2) 設正數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,其中
,其中![]() ,數列
,數列![]() 中的前
中的前![]() 項:
項:![]() 組成的集合
組成的集合![]() 記作
記作![]() ,將集合
,將集合![]() 中的所有元素
中的所有元素![]() 從小到大排序,即
從小到大排序,即![]() 滿足
滿足![]() ,求
,求![]() ;
;
(3) 己知集合![]() ,其中數列
,其中數列![]() 是等比數列,
是等比數列,![]() ,且公比是有理數,判斷集合
,且公比是有理數,判斷集合![]() 是否具有性質
是否具有性質![]() ,說明理由.
,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率e滿足
的離心率e滿足![]() ,右頂點為A,上頂點為B,點C(0,-2),過點C作一條與y軸不重合的直線l,直線l交橢圓E于P,Q兩點,直線BP,BQ分別交x軸于點M,N;當直線l經過點A時,l的斜率為
,右頂點為A,上頂點為B,點C(0,-2),過點C作一條與y軸不重合的直線l,直線l交橢圓E于P,Q兩點,直線BP,BQ分別交x軸于點M,N;當直線l經過點A時,l的斜率為![]() .
.
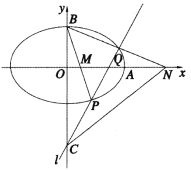
(1)求橢圓E的方程;
(2)證明:![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com