已知f(x)=-2x2+2ax-a2b.
(I)當不等式f(x)>0的解集為(-1,3)時,求實數a,b的值;
(Ⅱ)若對任意實數a,f(2)<0恒成立,求實數b的取值范圍;
(Ⅲ)設b使不為0的常數,解關于a的不等式f(1)+ab<0.
【答案】
分析:(I)將不等式f(x)>0的解集為(-1,3),轉化為-1,3是方程-2x
2+2ax-a
2b=0的兩個根,從而可求a=2,b=
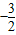
;
(Ⅱ)對任意實數a,f(2)<0恒成立,等價于-8+4a-a
2b0對任意實數a恒成立,從而可求實數b的取值范圍;
(Ⅲ)f(1)+ab<0,即-2+2a-a
2b+ab0,對參數b進行討論,可解不等式.
解答:解:(I)∵不等式f(x)>0的解集為(-1,3),
∴-1,3是方程-2x
2+2ax-a
2b=0的兩個根
∴
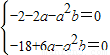
∴a=2,b=
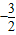
;
(Ⅱ)對任意實數a,f(2)<0恒成立,等價于-8+4a-a
2b<0對任意實數a恒成立
即ba
2-4a+8>0對任意實數a恒成立
∴
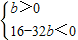
∴
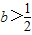
;
(Ⅲ)f(1)+ab<0,即-2+2a-a
2b+ab<0
∴ba
2-(2+b)+2>0
∴(ba-2)(a-1)>0
當b<0時,
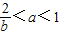
當0<b<2時,a<1,或
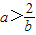
當b=2時a≠1
當b>2時,
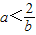
,或a>1
點評:本題以函數為載體,考查不等式解集與方程根的關系,考查二次不等式恒成立問題,考查解不等式,正確分類是關鍵.

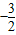 ;
;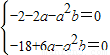
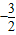 ;
;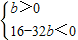
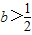 ;
;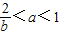
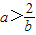
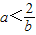 ,或a>1
,或a>1

 閱讀快車系列答案
閱讀快車系列答案