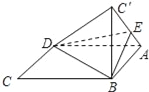
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】如圖，將菱形ABCD沿對角線BD折起，使得C點至C′，E點在線段AC′上，若二面角A﹣BD﹣E與二面角E﹣BD﹣C′的大小分別為15°和30°，則__．

【答案】

【解析】

取BD的中點O，連接AO，EO，C′O，由題設知AOE=15°，∠EOC′=30°，由此利用正弦定理能求出．

取BD的中點O，連接AO，EO，C′O，

∵菱形ABCD沿對角線BD折起，使得C點至C′，E點在線段AC′上，

∴C′O⊥BD，AO⊥BD，OC′=OA，

∴BD⊥平面AOC′，

∴EO⊥BD，

∵二面角A﹣BD﹣E與二面角E﹣BD﹣C′的大小分別為15°和30°，

∴∠AOE=15°，∠EOC′=30°，

∵OC′=OA，∴∠OC′E=∠OAE，

由正弦定理得，，

∴，

∴===．

故答案為：．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】在△ABC中，∠A=60°，c= a．（13分）
（1）求sinC的值；
（2）若a=7，求△ABC的面積．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知等差數列{an}的前n項和為Sn ， 等比數列{bn}的前n項和為Tn ， a1=﹣1，b1=1，a2+b2=2．
（Ⅰ）若a3+b3=5，求{bn}的通項公式；
（Ⅱ）若T3=21，求S3 ．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知a＞0，b＞0，a3+b3=2，證明：
（Ⅰ）（a+b）（a5+b5）≥4；
（Ⅱ）a+b≤2．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知F為拋物線C：y2=4x的焦點，過F作兩條互相垂直的直線l1 ， l2 ， 直線l1與C交于A、B兩點，直線l2與C交于D、E兩點，則|AB|+|DE|的最小值為（　　）
A.16
B.14
C.12
D.10

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖,四面體中, 是正三角形, 是直角三角形, ,.

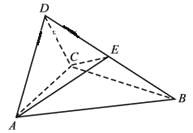
（1）證明:平面平面;

（2）過的平面交于點,若平面把四面體分成體積相等的兩部分,求二面角的大小。

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知圓M過C(1,-1),D(-1,1)兩點，且圓心M在x+y-2=0上．

（1）求圓M的方程；

（2）設點P是直線3x+4y+8=0上的動點，PA,PB是圓M的兩條切線，A,B為切點，求四邊形PAMB面積的最小值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖程序框圖是為了求出滿足3n﹣2n＞1000的最小偶數n，那么在 和 兩個空白框中，可以分別填入（　　）

A.A＞1000和n=n+1
B.A＞1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．
（Ⅰ）求a；
（Ⅱ）證明：f（x）存在唯一的極大值點x0 ， 且e﹣2＜f（x0）＜2﹣2 ．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产精品久久久久久久久久妞妞 | 99爱在线观看 | 欧美h视频 | 五月婷婷综合激情 | 久干网| 99热这里 | 亚洲国产精品一区二区三区 | 欧美视频亚洲视频 | 久久不卡日韩美女 | 中文字幕在线电影 | 日韩性视频 | 久久精品久久久久久久 | 91成人免费在线视频 | 欧美激情三级 | 久久视频免费在线 | 91精品国产综合久久久蜜臀粉嫩 | 91视频在线免费观看 | 毛片搜索| 久久伊人操 | 牛牛精品 | 精品国产视频 | 国产精品㊣新片速递bt | 国产丝袜一区二区三区免费视频 | 欧美中文字幕一区 | 国产精品乱码一区二区三区 | av网站免费 | 乱操视频 | 亚洲欧美日韩在线一区 | 亚州精品成人 | 国产午夜精品美女视频明星a级 | 中文字幕亚洲精品 | 日本激情网| 国产天天操 | 日韩精品免费一区二区在线观看 | 国产一区二区免费视频 | 亚洲欧美一区二区三区视频 | 国产二区视频 | 91精品国产色综合久久 | 日韩一区二区三区在线观看 | 免费的色网站 | 欧美在线播放一区 |