【題目】設數列{an}的前n項和為Sn，且Sn＝3an＋1(n∈N*).
(1)求數列{an}的通項公式；
(2)若數列{bn}滿足
，求數列{bn}的前n項和Tn.
【答案】（1）
；（2）
【解析】試題分析：
（1）在已知等式
中，令
可求得
，用
代替
可得
，兩式相減，可得
，從而知
是等比數列，從而得通項公式；
（2）由（1）可得
，因此可用錯位相減法求得其前
項和
．
試題解析：
(Ⅰ)當n≥2時，an＝Sn－Sn－1＝3an＋1－3an－1－1，
即2an＝3an－1，所以
＝
，
當n＝1時，a1＝3a1＋1，解得a1＝－
.
所以數列{an}是以－為首項，為公比的等比數列，即an＝－×
.
(2)由(1)可得bn＝－
×
所以Tn＝3×＋5×
＋…＋(2n－1) 
＋(2n＋1)， ①
Tn＝3×＋5×＋…＋(2n－1)＋(2n＋1) 
， ②
則①—②，得Tn＝3×＋2×
－(2n＋1) ，
化簡整理可得Tn＝5－
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且在
軸上的頂點分別為
，
.
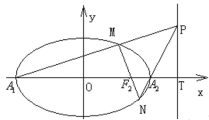
（1）求橢圓的方程；
（2）若直線
與軸交于點
，點
為直線
上異于點的任一點，直線
分別與橢圓交于
點，試問直線
能否通過橢圓的焦點？若能，求出
的值，若不能，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）如圖所示的莖葉圖記錄了甲、乙兩組各四名同學的投籃命中次數, 乙組記錄中有一個數據模糊，無法確認, 在圖中以
表示.
（Ⅰ）如果乙組同學投籃命中次數的平均數為
, 求及乙組同學投籃命中次數的方差;
（Ⅱ）在（Ⅰ）的條件下, 分別從甲、乙兩組投籃命中次數低于10次的同學中,各隨機選取一名, 記事件A：“兩名同學的投籃命中次數之和為17”, 求事件A發生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，
是兩條不同的直線，
，
，
是三個不同的平面，給出下列四個命題：
①若
，
，則
②若
，
，，則
③若
，，則
④若
，
，則
其中正確命題的序號是（ ）
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，直線
與圓C相切，圓心C的坐標為
（1）求圓C的方程；
（2）設直線y=x+m與圓C交于M、N兩點.
①若
，求m的取值范圍；
②若OM⊥ON，求m的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年“十一”期間，高速公路車輛較多．某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查，將他們在某段高速公路的車速（
）分成六段： 
， 
， 
， 
， 
， 
，后得到如圖的頻率分布直方圖．
（1）求這40輛小型車輛車速的眾數和中位數的估計值；
（2）若從車速在
的車輛中任抽取2輛，求車速在的車輛恰有一輛的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】孝感車天地關于某品牌汽車的使用年限
（年）和所支出的維修費用
（千元）由如表的統計資料：
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
（1）畫出散點圖并判斷使用年限與所支出的維修費用是否線性相關；如果線性相關，求回歸直線方程；
（2）若使用超過8年，維修費用超過1.5萬元時，車主將處理掉該車，估計第10年年底時，車主是否會處理掉該車？
（
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，點
在橢圓
上.
(1)求橢圓的方程；
(2)若不過原點
的直線
與橢圓相交于
兩點，與直線
相交于點
，且是線段
的中點，求
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
