日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

若橢圓的兩個焦點為F1(－4，0)、F2(4，0)，橢圓的弦AB過點F1，且△ABF2的周長為20，那么該橢圓的方程為__________.

+=1


解析:

△ABF2的周長:|AF2|+|AF1|+|BF2|+|BF1|=2a+2a=4a=20,

∴a=5.又∵c=4,∴b=3.

∴橢圓的方程為+=1.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知橢圓C：
x2
a2
+
y2
b2
=1(a＞b＞0)的兩個焦點為F1（-1，0），F2（1，0），點P(
3
3
，
11
2
)在橢圓C上．
（Ⅰ）求橢圓C的方程；
（Ⅱ）記O為坐標原點，過F2（1，0）的直線l與橢圓C相交于E，F兩點，若△OEF的面積為
6
2
7
，求直線l的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：

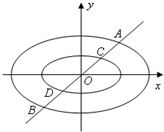精英家教網定義：由橢圓的兩個焦點和短軸的一個頂點組成的三角形稱為該橢圓的“特征三角形”．如果兩個橢圓的“特征三角形”是相似的，則稱這兩個橢圓是“相似橢圓”，并將三角形的相似比稱為橢圓的相似比．已知橢圓C1：
x2
4
+y2=1．
（1）若橢圓C2：
x2
16
+
y2
4
=1，判斷C2與C1是否相似？如果相似，求出C2與C1的相似比；如果不相似，請說明理由；
（2）寫出與橢圓C1相似且短半軸長為b的橢圓Cb的方程；若在橢圓Cb上存在兩點M、N關于直線y=x+1對稱，求實數b的取值范圍？
（3）如圖：直線y=x與兩個“相似橢圓”M：
x2
a2
+
y2
b2
=1和Mλ：
x2
a2
+
y2
b2
=λ2(a＞b＞0，0＜λ＜1)分別交于點A，B和點C，D，試在橢圓M和橢圓Mλ上分別作出點E和點F（非橢圓頂點），使△CDF和△ABE組成以λ為相似比的兩個相似三角形，寫出具體作法．（不必證明）

查看答案和解析>>

科目：高中數學 來源： 題型：

（2011•淄博二模）橢圓C：
x2
a2
+
y2
b2
=1（a＞b＞0）的兩個焦點為F1、F2，短軸兩端點B1、B2，已知F1、F2、B1、B2四點共圓，且點N（0，3）到橢圓上的點最遠距離為5
2
．
（1）求此時橢圓C的方程；
（2）設斜率為k（k≠0）的直線m與橢圓C相交于不同的兩點E、F，Q為EF的中點，問E、F兩點能否關于過點P（0，
3
3
）、Q的直線對稱？若能，求出k的取值范圍；若不能，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

設雙曲線C以橢圓
x2
25
+
y2
9
=1的兩個焦點為焦點，且雙曲線C的焦點到其漸近線的距離為2
3
．
（1）求雙曲線C的方程；
（2）若直線y=kx+m（k≠0，m≠0）與雙曲線C交于不同的兩點E，F，且E，F都在以P（0，3）為圓心的同一圓上，求實數m的取信范圍．

查看答案和解析>>

科目：高中數學 來源：2010-2011學年浙江省臺州中學高三（上）第二次統練數學試卷（理科）（解析版） 題型：解答題

已知點F1，F2為橢圓的兩個焦點，點O為坐標原點，圓O是以F1，F2為直徑的圓，一條直線與圓O相切并與橢圓交于不同的兩點A，B．
（1）設b=f（k），求f（k）的表達式；
（2）若，求直線l的方程；
（3）若，求三角形OAB面積的取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久成人在线 | 91麻豆精品国产91久久久资源速度 | 久久久久a| 久久免费国产精品 | 婷婷在线视频 | 九九免费视频 | 欧美日韩在线看 | 国产精品一区二区在线播放 | 日韩不卡一区二区 | 毛片毛片毛片毛片毛片毛片 | 国产乱码精品一区二区三区手机版 | 91精品国产综合久久精品 | 亚洲三级网站 | 国产色av | 久久之精品| 成人久久免费 | 久久久久久一区二区 | 日本成年人免费网站 | a毛片在线免费观看 | 日本视频不卡 | 在线成人 | 仙人掌旅馆在线观看 | 狠狠综合久久av一区二区老牛 | 中文字幕一区二区三区免费视频 | 国产欧美久久久久久 | 午夜国产精品视频 | 香蕉视频91| 国产精品毛片大码女人 | 亚洲www永久成人夜色 | 日本黄色片免费 | 91视频观看 | 亚洲国产精品99 | 久久99国产精品久久99大师 | 国产精品无码永久免费888 | 情五月 | 色玖玖综合 | 最新午夜 | 免费 视频 1级 | 99久久精品国产一区二区三区 | 国产三区在线成人av | www.久久久.com |