
【題目】已知函數f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四個實數根,則t的取值范圍
【答案】![]()
【解析】f(x)=|xex|=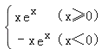
當x≥0時,f′(x)=ex+xex≥0恒成立,所以f(x)在[0,+∞)上為增函數;
當x<0時,f′(x)=﹣ex﹣xex=﹣ex(x+1),
由f′(x)=0,得x=﹣1,當x∈(﹣∞,﹣1)時,f′(x)=﹣ex(x+1)>0,f(x)為增函數,
當x∈(﹣1,0)時,f′(x)=﹣ex(x+1)<0,f(x)為減函數,
所以函數f(x)=|xex|在(﹣∞,0)上有一個極大值為f(﹣1)=﹣(﹣1)e﹣1=![]() ,
,
要使方程f2(x)+tf(x)+1=0(t∈R)有四個實數根,
令f(x)=m,則方程m2+tm+1=0應有兩個不等根,且一個根在(0,![]() )內,一個根在(
)內,一個根在(![]() ,+
,+![]() )內,
)內,
再令g(m)=m2+tm+1,
因為g(0)=1>0,
則只需g(![]() )<0,即
)<0,即![]() , 解得:t<﹣
, 解得:t<﹣![]() .
.
所以,使得函數f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四個實數根的t的取值范圍
是![]() .
.
故答案為![]() .
.
函數f(x)=|xex|是分段函數,通過求導分析得到函數f(x)在(0,+∞)上為增函數,在(﹣∞,﹣1)上為增函數,在(﹣1,0)上為減函數,求得函數f(x)在(﹣∞,0)上,當x=﹣1時有一個最大值![]() , 所以,要使方程f2(x)+tf(x)+1=0(t∈R)有四個實數根,f(x)的值一個要在(0,
, 所以,要使方程f2(x)+tf(x)+1=0(t∈R)有四個實數根,f(x)的值一個要在(0,![]() )內,一個在(
)內,一個在(![]() ,+
,+![]() )內,然后運用二次函數的圖象及二次方程根的關系列式求解t的取值范圍.
)內,然后運用二次函數的圖象及二次方程根的關系列式求解t的取值范圍.


科目:高中數學 來源: 題型:
【題目】研究發現,北京 PM 2.5 的重要來源有土壤塵、燃煤、生物質燃燒、汽車尾氣與垃圾焚燒、工業污染和二次無機氣溶膠,其中燃煤的平均貢獻占比約為 18%.為實現“節能減排”,還人民“碧水藍天”,北京市推行“煤改電”工程,采用空氣源熱泵作為冬天供暖.進入冬季以來,該市居民用電量逐漸增加,為保證居民取暖,市供電部門對該市 100 戶居民冬季(按 120 天計算)取暖用電量(單位:度)進行統計分析,得到居民冬季取暖用電量的頻率分布直方圖如圖所示.

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)從這 100 戶居民中隨機抽取 1 戶進行深度調查,求這戶居民冬季取暖用電量在[3300,3400]的概率;
(3)在用電量為[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四組居民中,用分層抽樣的方法抽取 34 戶居民進行調查,則應從用電量在[3200,3250)的居民中抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C: ![]() (a>0,b>0)的左、右焦點分別為F1 , F2 , 點M與雙曲線C的焦點不重合,點M關于F1 , F2的對稱點分別為A,B,線段MN的中點在雙曲線的右支上,若|AN|﹣|BN|=12,則a=( )
(a>0,b>0)的左、右焦點分別為F1 , F2 , 點M與雙曲線C的焦點不重合,點M關于F1 , F2的對稱點分別為A,B,線段MN的中點在雙曲線的右支上,若|AN|﹣|BN|=12,則a=( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下結論,其中正確結論的個數為( )
①函數![]() 的零點為
的零點為![]() ,則函數
,則函數![]() 的圖象經過點
的圖象經過點![]() 時,函數值一定變號.
時,函數值一定變號.
②相鄰兩個零點之間的所有函數值保持同號.
③函數![]() 在區間
在區間![]() 上連續,若滿足
上連續,若滿足![]() ,則方程
,則方程![]() 在區間
在區間![]() 上一定有實根.
上一定有實根.
④“二分法”對連續不斷的函數的所有零點都有效.
A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}共有5項,其中a1=0,a5=2,且|ai+1﹣ai|=1,i=1,2,3,4,則滿足條件的不同數列的個數為( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() (其中a∈R).
(其中a∈R).
(1)討論函數f(x)的奇偶性,并說明理由.
(2)若![]() ,試判斷函數f(x)在區間[1,+∞)上的單調性,并用函數單調性定義給出證明.
,試判斷函數f(x)在區間[1,+∞)上的單調性,并用函數單調性定義給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,點
底面ABCD,點![]() 、F分別是線段
、F分別是線段![]() 、BC的中點.
、BC的中點.
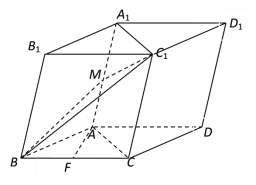
(1)求證:AF//平面![]() ;
;
(2)求證:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位.若直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位.若直線![]() 的參數方程為
的參數方程為![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(II)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若
兩點,若![]() 點的直角坐標為
點的直角坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com