
【題目】某公園劃船收費標準如表:

某班16名同學一起去該公園劃船,若每人劃船的時間均為1小時,每只租船必須坐滿,租船最低總費用為______元,租船的總費用共有_____種可能.
科目:高中數學 來源: 題型:
【題目】2019年10月1日我國隆重紀念了建國70周年,期間進行了一系列大型慶祝活動,極大地激發了全國人民的愛國熱情.某校高三學生也投入到了這場愛國活動中,他(她)們利用周日休息時間到社區做義務宣講員,學校為了調查高三男生和女生周日的活動時間情況,隨機抽取了高三男生和女生各40人,對他(她)們的周日活動時間進行了統計,分別得到了高三男生的活動時間(單位:小時)的頻數分布表和女生的活動時間(單位:小時)的頻率分布直方圖.(活動時間均在![]() 內)
內)
活動時間 |
|
|
|
|
|
|
頻數 | 8 | 10 | 7 | 9 | 4 | 2 |
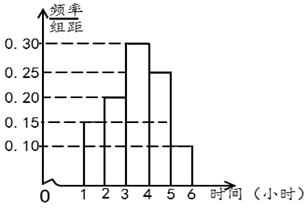
(1)根據調查,試判斷該校高三年級學生周日活動時間較長的是男生還是女生?并說明理由;
(2)在被抽取的80名高三學生中,從周日活動時間在![]() 內的學生中抽取2人,求恰巧抽到1男1女的概率.
內的學生中抽取2人,求恰巧抽到1男1女的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障某治療新冠肺炎藥品的主要藥理成分在國家藥品監督管理局規定的值范圍內,武漢某制藥廠在該藥品的生產過程中,檢驗員在一天中按照規定從該藥品生產線上隨機抽取20件產品進行檢測,測量其主要藥理成分含量(單位:mg).根據生產經驗,可以認為這條藥品生產線正常狀態下生產的產品的主要藥理成分含量服從正態分布N(μ,σ2).在一天內抽取的20件產品中,如果有一件出現了主要藥理成分含量在(μ﹣3σ,μ+3σ)之外的藥品,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對本次的生產過程進行檢查.
(1)下面是檢驗員在2月24日抽取的20件藥品的主要藥理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
經計算得![]() xi=9.96,s
xi=9.96,s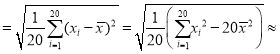 0.19;其中xi為抽取的第i件藥品的主要藥理成分含量,i=1,2,…,20.用樣本平均數
0.19;其中xi為抽取的第i件藥品的主要藥理成分含量,i=1,2,…,20.用樣本平均數![]() 作為μ的估計值
作為μ的估計值![]() ,用樣本標準差s作為σ的估計值
,用樣本標準差s作為σ的估計值![]() ,利用估計值判斷是否需對本次的生產過程進行檢查?
,利用估計值判斷是否需對本次的生產過程進行檢查?
(2)假設生產狀態正常,記X表示某天抽取的20件產品中其主要藥理成分含量在(μ﹣3σ,μ+3σ)之外的藥品件數,求/span>P(X=1)及X的數學期望.
附:若隨機變量Z服從正態分布N(μ,σ2),則P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.
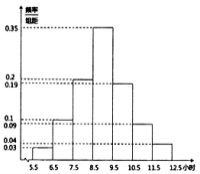
(1)求這200名學生每周閱讀時間的樣本平均數![]() 和中位數
和中位數![]() (
(![]() 的值精確到0.01);
的值精確到0.01);
(2)為查找影響學生閱讀時間的因素,學校團委決定從每周閱讀時間為![]() ,
,![]() 的學生中抽取9名參加座談會.
的學生中抽取9名參加座談會.
(i)你認為9個名額應該怎么分配?并說明理由;
(ii)座談中發現9名學生中理工類專業的較多.請根據200名學生的調研數據,填寫下面的列聯表,并判斷是否有![]() 的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
閱讀時間不足8.5小時 | 閱讀時間超過8.5小時 | |
理工類專業 | 40 | 60 |
非理工類專業 |
附:![]() (
(![]() ).
).
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 與曲線
與曲線![]() ,(
,(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)寫出曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,已知![]() 與
與![]() ,
,![]() 的公共點分別為
的公共點分別為![]() ,
,![]() ,
,![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于正整數![]() ,如果
,如果![]() 個整數
個整數![]() 滿足
滿足![]() ,
,
且![]() ,則稱數組
,則稱數組![]() 為
為![]() 的一個“正整數分拆”.記
的一個“正整數分拆”.記![]() 均為偶數的“正整數分拆”的個數為
均為偶數的“正整數分拆”的個數為![]() 均為奇數的“正整數分拆”的個數為
均為奇數的“正整數分拆”的個數為![]() .
.
(Ⅰ)寫出整數4的所有“正整數分拆”;
(Ⅱ)對于給定的整數![]() ,設
,設![]() 是
是![]() 的一個“正整數分拆”,且
的一個“正整數分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)對所有的正整數![]() ,證明:
,證明:![]() ;并求出使得等號成立的
;并求出使得等號成立的![]() 的值.
的值.
(注:對于![]() 的兩個“正整數分拆”
的兩個“正整數分拆”![]() 與
與![]() ,當且僅當
,當且僅當![]() 且
且![]() 時,稱這兩個“正整數分拆”是相同的.)
時,稱這兩個“正整數分拆”是相同的.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() 的展開圖如圖二,其中四邊形
的展開圖如圖二,其中四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
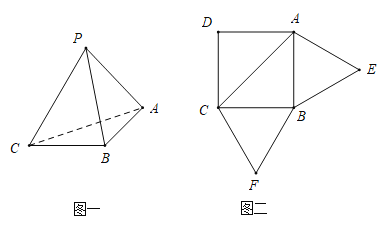
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com