
分析 (Ⅰ)求出函數的導數,通過解關于導函數的不等式,求出函數的單調區間即可;
(Ⅱ)(i)求出g(x)的導數,得到關于a,b的方程組,解出即可;
(ii)問題轉化為g(x)-k(x2-x)>0對x∈(0,+∞)恒成立.令F(x)=g(x)-k(x2-x),求出函數的導數,通過討論k的范圍,求出函數的單調區間,從而確定k的范圍即可.
解答 解:(Ⅰ)當a=1,b=-1時,f(x)=ln(1+x)-x,(x>-1),
則$f'(x)=\frac{1}{1+x}-1=\frac{-x}{1+x}$.
當f'(x)>0時,-1<x<0;
當f'(x)<0時,x>0;
所以f(x)的單調增區間為(-1,0),單調減區間為(0,+∞).…(4分)
(Ⅱ)( i)因為g(x)=f(x)-bx2=ln(1+ax)+b(x-x2),
所以$g'(x)=\frac{a}{1+ax}+b(1-2x)$.
依題設有$\left\{\begin{array}{l}g(1)=ln(1+a)\\ g'(1)=\frac{11}{3}\end{array}\right.$即$\left\{\begin{array}{l}ln(1+a)=ln3\\ \frac{a}{1+a}-b=\frac{11}{3}.\end{array}\right.$
解得$\left\{\begin{array}{l}a=2\\ b=-3\end{array}\right.$.…(8分)
( ii))所以$g(x)=ln(1+2x)-3(x-{x^2}),x∈(-\frac{1}{2},+∞)$.
g(x)>k(x2-x)對x∈(0,+∞)恒成立,
即g(x)-k(x2-x)>0對x∈(0,+∞)恒成立.
令F(x)=g(x)-k(x2-x).
則有$F'(x)=\frac{{4(3-k){x^2}+k-1}}{1+2x}$.
①當1≤k≤3時,當x∈(0,+∞)時,F'(x)>0,
所以F(x)在(0,+∞)上單調遞增.
所以F(x)>F(0)=0,即當x∈(0,+∞)時,g(x)>k(x2-x);
②當k<1時,當$x∈(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$時,F'(x)<0,
所以F(x)在$(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$上單調遞減,
故當$x∈(0,\frac{1}{2}\sqrt{\frac{1-k}{3-k}})$時,F(x)<F(0)=0,
即當x∈(0,+∞)時,g(x)>k(x2-x)不恒成立.
綜上,k∈[1,3]. …(13分)
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想,是一道中檔題.


科目:高中數學 來源: 題型:選擇題
 某四棱錐的三視圖如圖所示,其俯視圖為等腰直角三角形,則該四棱錐的體積為( )
某四棱錐的三視圖如圖所示,其俯視圖為等腰直角三角形,則該四棱錐的體積為( )| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 9 | B. | 13 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
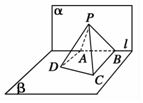 如圖,已知平面α⊥β,α∩β=l,A,B是直線l上的兩點,C,D是平面β內的兩點,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一動點,且直線 PD,PC與平面α所成角相等,則二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如圖,已知平面α⊥β,α∩β=l,A,B是直線l上的兩點,C,D是平面β內的兩點,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一動點,且直線 PD,PC與平面α所成角相等,則二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com