
 遞減;
遞減; ;
; .
. ,x>0.由f′(x)=2x-
,x>0.由f′(x)=2x- =0,x>0,得x=
=0,x>0,得x= ,列表討論,能求出f(x)=h(x)-m(x)在
,列表討論,能求出f(x)=h(x)-m(x)在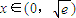 遞減;
遞減; ),把(
),把( )代入y=x+b,得b=-
)代入y=x+b,得b=- ,故h(x)和φ(x)存在“隔離直線”y=kx+b,且b的最大值為
,故h(x)和φ(x)存在“隔離直線”y=kx+b,且b的最大值為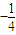 ;
;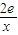 ,x>0.由f′(x)=2x-
,x>0.由f′(x)=2x- =0,x>0,得x=
=0,x>0,得x= ,
,| x | (0, ) ) |  | ( ) ) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 極小值 | ↑ |
 遞減,故①正確;
遞減,故①正確; ),
), )代入y=x+b,得b=-
)代入y=x+b,得b=- ,
,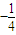 ,故③正確;
,故③正確;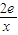 =0,x>0,得x=
=0,x>0,得x=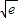 ,
,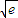 處有公共點.
處有公共點. ),即y=kx-k
),即y=kx-k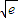 +e.
+e. +e可得 x2-kx+k
+e可得 x2-kx+k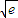 -e≥0當x∈R恒成立,
-e≥0當x∈R恒成立, +4e=(k-2
+4e=(k-2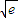 )2≤0,只有k=2
)2≤0,只有k=2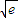 時,等號成立,此時直線方程為:y=2
時,等號成立,此時直線方程為:y=2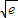 x-e.
x-e.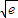 +e,可得只有k=2
+e,可得只有k=2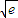 時,等號成立,此時直線方程為:y=2
時,等號成立,此時直線方程為:y=2 x-e.
x-e. x-e,故④正確.
x-e,故④正確.

 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| e |
| e |
查看答案和解析>>
科目:高中數學 來源: 題型:
| e |
| 1 |
| 4 |
| e |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省廣州市執信中學高三(上)期中數學試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三12月練習數學試卷 題型:填空題
若存在實常數k和b,使函數 和
和 對其定義域上的任意實數x恒有:
對其定義域上的任意實數x恒有:
 和
和 ,則稱直線
,則稱直線 為
為 和
和 的“隔離直線”。
的“隔離直線”。
已知 ,則可推知
,則可推知 的“隔離直線”方程為 ▲
的“隔離直線”方程為 ▲
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com