【答案】
分析:(1)因為對角線互相垂直的四邊形ABCD面積

,由于|AC|=d為定長,當|BD|最大時,四邊形ABCD面積S取得最大值.由圓的性質,垂直于AC的弦中,直徑最長,由此能求出四邊形ABCD面積的最大值.
(2)由題意,當點P運動到與圓心M重合時,對角線AC和BD的長同時取得最大值|AC|=|BD|=2r,由此能求出四邊形ABCD面積S取得最大值,最大值為2r
2.
(3)類比猜想1:若對角線互相垂直的橢圓內接四邊形ABCD中的一條對角線長確定時,當且僅當另一條對角線通過橢圓中心時,該橢圓內接四邊形面積最大;類比猜想2:當點P在橢圓中心時,對角線互相垂直的橢圓內接四邊形ABCD的面積最大;以上兩個均為正確的猜想,要證明以上兩個猜想,都需先證:橢圓內的平行弦中,過橢圓中心的弦長最大.類比猜想3:當點P•在橢圓中心,且橢圓內接四邊形的兩條互相垂直的對角線恰為橢圓長軸和短軸時,四邊形面積取得最大值2ab.要證明此猜想,也需先證“橢圓內的平行弦中,過橢圓中心的弦長最大.”
解答:解:(1)因為對角線互相垂直的四邊形ABCD面積
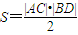
,
而由于|AC|=d為定長,
則當|BD|最大時,四邊形ABCD面積S取得最大值.由圓的性質,垂直于AC的弦中,直徑最長,
故當且僅當BD過圓心M時,四邊形ABCD面積S取得最大值,最大值為dr.
(2)由題意,不難發現,當點P運動到與圓心M重合時,對角線AC和BD的長同時取得最大值|AC|=|BD|=2r,
所以此時四邊形ABCD面積S取得最大值,最大值為2r
2.
(3)類比猜想1:若對角線互相垂直的橢圓內接四邊形ABCD中的一條對角線長確定時,當且僅當另一條對角線通過橢圓中心時,該橢圓內接四邊形面積最大.
類比猜想2:當點P在橢圓中心時,對角線互相垂直的橢圓內接四邊形ABCD的面積最大.
以上兩個均為正確的猜想,要證明以上兩個猜想,都需先證:橢圓內的平行弦中,過橢圓中心的弦長最大.
證:設橢圓的方程為
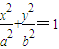
(a>b>0),平行弦MN的方程為y=kx+m,
聯立可得b
2x
2+a
2(kx+m)
2-a
2b
2=0⇒(b
2+a
2k
2)x
2+2kma
2x+m
2a
2-a
2b
2=0
不妨設M(x
1,y
1)、N(x
2,y
2),
則
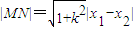
=
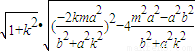
=

=
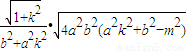
由于平行弦的斜率k保持不變,故可知當且僅當m=0時,即當直線經過原點時,
|MN|取得最大值
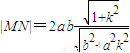
(*).特別地,當斜率不存在時,此結論也成立.
由以上結論可知,類比猜想一正確.又對于橢圓內任意一點P構造的對角線互相垂直的橢圓內接四邊形,我們都可以將對角線平移到交點與橢圓中心O重合的橢圓內接四邊形A
1B
1C
1D
1,而其中|AC|≤|A
1C
1|,|BD|≤|B
1D
1|,
所以必有

.即證明了猜想二也是正確的.
類比猜想3:當點P•在橢圓中心,且橢圓內接四邊形的兩條互相垂直的對角線恰為橢圓長軸和短軸時,四邊形面積取得最大值2ab.
要證明此猜想,也需先證“橢圓內的平行弦中,過橢圓中心的弦長最大.”在此基礎上,可參考以下兩種續證方法.
證法一:當點P在橢圓中心時,不妨設對角線AC所在直線的斜率為k.
(i)當k=0時,AC即為橢圓長軸,又AC⊥BD,故BD是橢圓的短軸.
所以此時橢圓內接四邊形ABCD的面積為S
ABCD=2ab.
(ii)當k≠0時,對角線BD的斜率為
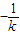
.由此前證明過程中的(*)可知,
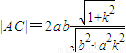
,
若將
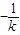
代換式中的k,則可得弦BD的長度,
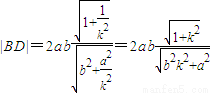
.
所以,
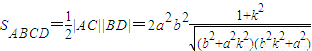
=
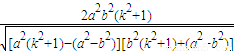
=
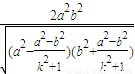
=
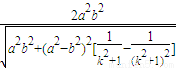
=
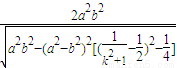
由k
2+1>1⇒
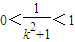
⇒
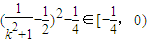
,
則
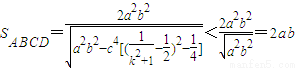
,
綜上(i)和(ii),故可證明猜想三正確.
證法二:如圖,四邊形對角線交點P與橢圓中心重合.
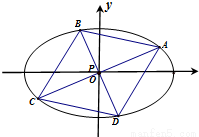
由對稱性,不妨設橢圓上的點A的坐標為(acosα,bsinα),
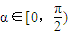
;
相鄰的點B坐標為(acosβ,bsinβ),
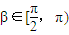
.由對稱性可知,

且當
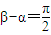
時,S
ABCD取得最大值2ab.
又因為OA⊥OB,故
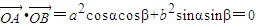
.
由
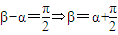
,
所以
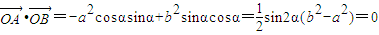
故只有當sin2α=0時才滿足,
而因為
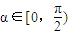
,
故只有當α=0時成立.即由橢圓參數方程的定義,當且僅當點A和點B分別落在橢圓長軸和短軸頂點上時,猜想3正確.
點評:本題考查直線和圓錐曲線的綜合運用,解題時要認真審題,注意挖掘題設中的隱含條件,合理地進行類比猜想.

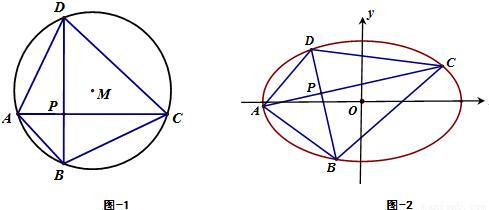
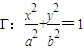 (a>b>0)的內接四邊形ABCD的對角線AC和BD相互垂直且交于點P.試提出一個由類比獲得的猜想,并嘗試給予證明或反例否定.
(a>b>0)的內接四邊形ABCD的對角線AC和BD相互垂直且交于點P.試提出一個由類比獲得的猜想,并嘗試給予證明或反例否定. ,由于|AC|=d為定長,當|BD|最大時,四邊形ABCD面積S取得最大值.由圓的性質,垂直于AC的弦中,直徑最長,由此能求出四邊形ABCD面積的最大值.
,由于|AC|=d為定長,當|BD|最大時,四邊形ABCD面積S取得最大值.由圓的性質,垂直于AC的弦中,直徑最長,由此能求出四邊形ABCD面積的最大值.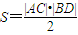 ,
,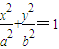 (a>b>0),平行弦MN的方程為y=kx+m,
(a>b>0),平行弦MN的方程為y=kx+m,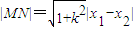
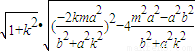

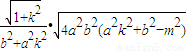
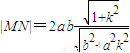 (*).特別地,當斜率不存在時,此結論也成立.
(*).特別地,當斜率不存在時,此結論也成立. .即證明了猜想二也是正確的.
.即證明了猜想二也是正確的.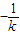 .由此前證明過程中的(*)可知,
.由此前證明過程中的(*)可知,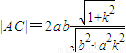 ,
,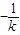 代換式中的k,則可得弦BD的長度,
代換式中的k,則可得弦BD的長度,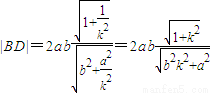 .
.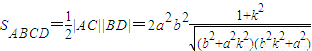
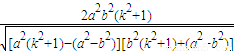
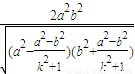
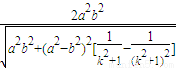
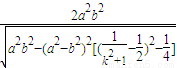
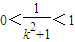 ⇒
⇒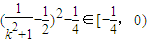 ,
,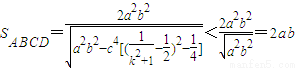 ,
,
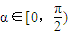 ;
;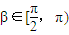 .由對稱性可知,
.由對稱性可知,
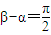 時,SABCD取得最大值2ab.
時,SABCD取得最大值2ab.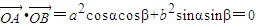 .
.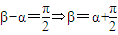 ,
,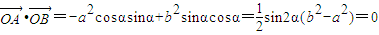
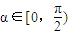 ,
,

 優等生題庫系列答案
優等生題庫系列答案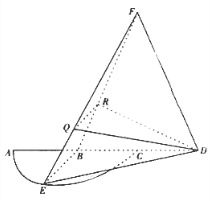 如圖,
如圖,


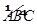 是半徑為a的半圓,AC為直徑,點E為
是半徑為a的半圓,AC為直徑,點E為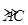 的中點,點B和點C為線段AD的三等分點.平面AEC外一點F滿足
的中點,點B和點C為線段AD的三等分點.平面AEC外一點F滿足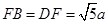 ,FE=
,FE=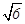 a
.
a
.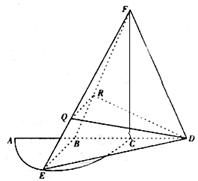
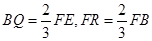 ,求平面
,求平面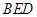 與平面
與平面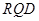 所成二面角的正弦值
所成二面角的正弦值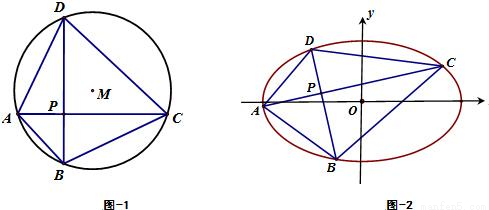
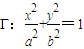 (a>b>0)的內接四邊形ABCD的對角線AC和BD相互垂直且交于點P.試提出一個由類比獲得的猜想,并嘗試給予證明或反例否定.
(a>b>0)的內接四邊形ABCD的對角線AC和BD相互垂直且交于點P.試提出一個由類比獲得的猜想,并嘗試給予證明或反例否定.