分析:和定積最大,直接運用均值不等式2/x+8/y=1≥2
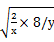
=8
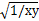
,就可解得xy的最小值,注意等號成立的條件。
解答:
因為x>0,y>0
所以
2/x+8/y=1≥2
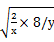
=8
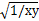
,
?xy≥64當且僅當x=4,y=16時取等號,
故選A。
點評:本題考查了均值不等式,定理的使用條件為一正二定三相等,利用基本不等式可求最值,和定積最大,積定和最小。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
已知a > 0,b > 0,a、b的等差中項是

,且

,則x + y的最小值是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
某校伙食長期以面粉和大米為主食,面食每100 g含蛋白質6個單位,含淀粉4個單位,售價0.5元,米食每100 g含蛋白質3個單位,含淀粉7個單位,售價0.4元,學校要求給學生配制盒飯,每盒盒飯至少有8個單位的蛋白質和10個單位的淀粉,問應如何配制盒飯,才既科學又費用最少?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
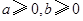
,且
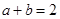
,則 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若x,y為正數(shù),且x+4y=3,求
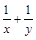
的最小值為( )
| A.3 | B.6 | C.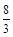 | D.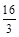 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設x,y為正實數(shù),且x+2y=1,則

的最小值為
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題12分)設
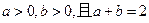
(1)求

的最大值;(2)求

最小值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設

在約束條件

下,目標函數(shù)

的最大值為4,則

的值為
.
查看答案和解析>>

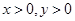 ,且
,且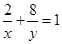 ,則
,則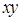 有( )
有( )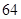
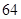
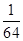
 閱讀快車系列答案
閱讀快車系列答案