
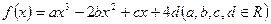 的圖象關(guān)于原點對稱,且
的圖象關(guān)于原點對稱,且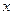 =1時,f(x)取極小值
=1時,f(x)取極小值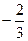 。
。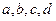 的值;
的值;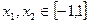 時,求證:
時,求證: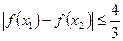 。
。 有f(-x)="-" f(x).
有f(-x)="-" f(x). . ∴f′(1)=0且f(1)="-"
. ∴f′(1)=0且f(1)="-"  ,
, +c=-
+c=- . 解得a=
. 解得a=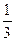 ,c=-1………………………………….6分
,c=-1………………………………….6分 , fmin(x)=f(1)= -
, fmin(x)=f(1)= - .
. .
. f(x1)-f(x2)|≤
f(x1)-f(x2)|≤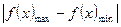 =
= +
+ =
=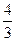 .
. ]時,|f(x1)-f(x2)|≤
]時,|f(x1)-f(x2)|≤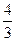 ………………………………………….12分
………………………………………….12分

科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
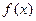 的定義域為開區(qū)間
的定義域為開區(qū)間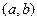 ,導(dǎo)函數(shù)
,導(dǎo)函數(shù)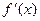 在
在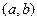 內(nèi)的圖象如
內(nèi)的圖象如 圖
圖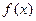 在開區(qū)間
在開區(qū)間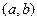 內(nèi)有駐點
內(nèi)有駐點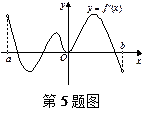

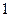 個 B
個 B
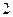 個 C
個 C
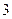 個 D
個 D
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com