
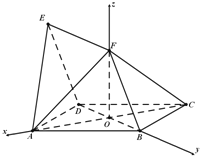
【題目】如圖,四邊形ABCD與BDEF均為菱形,∠DAB=∠DBF=60°,且FA=FC.
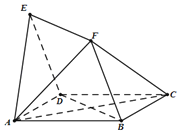
(Ⅰ)求證:AC⊥平面BDEF;
(Ⅱ)求證:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
【答案】(1)見解析(2)見解析(3)![]()
【解析】試題分析:(Ⅰ)設![]() 與
與![]() 相交于點
相交于點![]() ,連接
,連接![]() ,因為四邊形
,因為四邊形![]() 為菱形,所以
為菱形,所以![]() ,且
,且![]() 為
為![]() 中點,由
中點,由![]() ,知
,知![]() ,由此能夠證明
,由此能夠證明![]() 平面
平面![]() ;(Ⅱ)因為四邊形
;(Ⅱ)因為四邊形![]() 與
與![]() 均為菱形,所以
均為菱形,所以![]() ,平面
,平面![]() 平面
平面![]() ,由此能夠證明
,由此能夠證明![]() 平面
平面![]() ;(Ⅲ)因為四邊形
;(Ⅲ)因為四邊形![]() 為菱形,且
為菱形,且![]() ,所以
,所以![]() 為等邊三角形,因為
為等邊三角形,因為![]() 為
為![]() 中點,所以
中點,所以![]() ,故
,故![]() 平面
平面![]() ,由
,由![]() 兩兩垂直,建立空間直角坐標系
兩兩垂直,建立空間直角坐標系![]() ,設
,設![]() ,因為四邊形
,因為四邊形![]() 為菱形,
為菱形, ![]() ,則
,則![]() ,所以
,所以![]() ,
, ![]() ,求得平面
,求得平面![]() 的法向量為
的法向量為![]() ,平面
,平面![]() 的法向量為
的法向量為![]() ,由此能求出二面角
,由此能求出二面角![]() 的余弦值.
的余弦值.
試題解析:(Ⅰ)證明:設AC與BD相交于點O,
連接FO.因為四邊形ABCD為菱形,所以AC⊥BD,且O為AC中點.
又 FA=FC,所以 AC⊥FO.
因為 FO∩BD=O,
所以 AC⊥平面BDEF.
(Ⅱ)證明:因為四邊形ABCD與BDEF均為菱形,
所以AD∥BC,DE∥BF,
所以 平面FBC∥平面EAD.
又FC平面FBC,所以FC∥平面EAD.
(Ⅲ)解:因為四邊形BDEF為菱形,且∠DBF=60°,
所以△DBF為等邊三角形.
因為O為BD中點,所以FO⊥BD,故FO⊥平面ABCD.
由OA,OB,OF兩兩垂直,建立如圖所示的空間直角坐標系O﹣xyz. …(9分)
設AB=2.因為四邊形ABCD為菱形,∠DAB=60°,
則BD=2,所以OB=1,![]() .所以
.所以 ![]() .
.
所以 ![]() ,
,![]() .
.
設平面BFC的法向量為![]() =(x,y,z),
=(x,y,z),
則有![]() ,
,
取x=1,得![]() .
.
∵平面AFC的法向量為![]() =(0,1,0).
=(0,1,0).
由二面角A﹣FC﹣B是銳角,得|cos<![]() ,
,![]() >|=
>|=![]() =
=![]() .
.
所以二面角A﹣FC﹣B的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】函數f(x)=loga(1﹣x)+loga(x+3),(0<a<1).
(1)求函數f(x)的定義域;
(2)若函數f(x)的最小值為﹣2,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=x2+bx+c(b,c∈R,b<0).
(1)若f(x)的定義域為[0,1]時,值域也是[0,1],求b,c的值;
(2)若b=﹣2時,若函數g(x)= ![]() 對任意x∈[3,5],g(x)>c恒成立,試求實數c的取值范圍.
對任意x∈[3,5],g(x)>c恒成立,試求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信是騰訊公司推出的一種手機通訊軟件,它支持發送語音短信、視頻、圖片和文字,一經推出便風靡全國,甚至涌現出一批在微信的朋友圈內銷售商品的人(被稱為微商).為了調查每天微信用戶使用微信的時間,某經銷化妝品的微商在一廣場隨機采訪男性、女性用戶各50 名,其中每天玩微信超過6 小時的用戶列為“微信控”,否則稱其為“非微信控”,調查結果如下:
微信控 | 非微信控 | 合計 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據以上數據,能否有60%的把握認為“微信控”與”性別“有關?
(2)現從調查的女性用戶中按分層抽樣的方法選出5 人并從選出的5 人中再隨機抽取3 人贈送200 元的護膚品套裝,記這3 人中“微信控”的人數為X,試求X 的分布列與數學期望.
參考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來蓬勃發展的新機遇相關管理部門推出了針對電商的商品和服務的評價體系.現從評價系統中選出![]() 次成功交易,并對其評價進行統計愛,商品和服務評價的
次成功交易,并對其評價進行統計愛,商品和服務評價的![]() 列聯表如下表:
列聯表如下表:
對服務好評 | 對服務不滿意 | 合計 | |
對商品好評 |
|
|
|
對商品不滿意 |
|
|
|
合計 |
|
|
|
(1)是否可以在犯錯誤概率不超過![]() 的前提下,認為商品好評與服務好評有關?
的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的![]() 次購物中,設對商品和服務全好評的次數為隨機變量
次購物中,設對商品和服務全好評的次數為隨機變量![]() ,求
,求![]() 的數學期望.
的數學期望.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(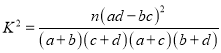 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批發市場對某種商品的日銷售量(單位:噸)進行統計,最近50天的統計結果如下:

若以上表中頻率作為概率,且每天的銷售量相互獨立.
(1)求5天中該種商品恰好有兩天的日銷售量為1.5噸的概率;
(2)已知每噸該商品的銷售利潤為2千元, ![]() 表示該種商品某兩天銷售利潤的和(單位:千元),求
表示該種商品某兩天銷售利潤的和(單位:千元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (a>b>0)的左、右焦點分別為F1,F2,點M(0,2)是橢圓的一個頂點,△F1MF2是等腰直角三角形.
(a>b>0)的左、右焦點分別為F1,F2,點M(0,2)是橢圓的一個頂點,△F1MF2是等腰直角三角形.
(1)求橢圓的方程;
(2)過點M分別作直線MA,MB交橢圓于A,B兩點,設兩直線的斜率分別為k1,k2,且k1+k2=8,證明:直線AB過定點![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com