
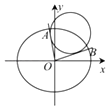
【題目】如圖所示,已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的焦距為2,直線y=x被橢圓C截得的弦長為
=1(a>b>0)的焦距為2,直線y=x被橢圓C截得的弦長為 ![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設點M(x0 , y0)是橢圓C上的動點,過原點O引兩條射線l1 , l2與圓M:(x﹣x0)2+(y﹣y0)2= ![]() 分別相切,且l1 , l2的斜率k1 , k2存在.
分別相切,且l1 , l2的斜率k1 , k2存在.
①試問k1k2是否定值?若是,求出該定值,若不是,說明理由;
②若射線l1 , l2與橢圓C分別交于點A,B,求|OA||OB|的最大值.
【答案】解:(Ⅰ)由2c=2,c=1,設直線直線y=x被與橢圓C相交于P,Q兩點,
則丨OP丨= ![]() ,設P(
,設P( ![]() ,
, ![]() ),代入橢圓方程,
),代入橢圓方程, ![]() ,①
,①
由a2﹣b2=1,②
解得:a2=2,b2=1,
∴橢圓的標準方程: ![]() ;
;
(Ⅱ)①設射線l的方程y=kx,A(x1 , y1),B(x2 , y2),
由 ![]() =
= ![]() ,兩邊平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
,兩邊平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
由y02=1﹣ ![]() ,
,
∴k1k2= ![]() =
= 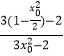 =﹣
=﹣ ![]() ,
,
∴k1k2為定值,定值﹣ ![]() ,
,
②方法一:聯立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
|OA|2|OB|2= ![]()
![]() =4×
=4× ![]() =
= ![]() =2+
=2+ ![]() ,
,
=2+ 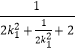 ≤
≤ ![]() ,當且僅當k12=
,當且僅當k12= ![]() ,取等號,
,取等號,
∴|OA||OB|的最大值為 ![]() ,
,
方法二:聯立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
則|OA|2+|OB|2= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =3,
=3,
由|OA|2+|OB|2≥2|OA||OB|,則|OA||OB|≤ ![]() ,當且僅當|OA|=|OB|時,取等號,
,當且僅當|OA|=|OB|時,取等號,
∴|OA||OB|的最大值 ![]() .
.
【解析】(Ⅰ)由c=2,求得P點坐標,代入橢圓方程,由a2﹣b2=1,即可求得a和b的值,即可求得橢圓方程;(Ⅱ)①設射線l的方程y=kx,代入橢圓方程,由韋達定理即可求得k1k2= ![]() ,由y02=1﹣
,由y02=1﹣ ![]() ,即可求得k1k2=﹣
,即可求得k1k2=﹣ ![]() ;②方法一:分別求得直線OA及OB的方程代入橢圓方程,求得|OA|及|OB|,利用基本不等式的性質,即可求得|OA||OB|的最大值;
;②方法一:分別求得直線OA及OB的方程代入橢圓方程,求得|OA|及|OB|,利用基本不等式的性質,即可求得|OA||OB|的最大值;
方法二:|OA|2+|OB|2= ![]() +
+ ![]() ,y02=1﹣
,y02=1﹣ ![]() ,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
【考點精析】解答此題的關鍵在于理解橢圓的標準方程的相關知識,掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設△ABC的內角A、B、C的對邊分別為a、b、c,且滿足sinA+sinB=[cosA﹣cos(π﹣B)]sinC.
(1)試判斷△ABC的形狀,并說明理由;
(2)若a+b+c=1+ ![]() ,試求△ABC面積的最大值.
,試求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某班舉行的“慶五一”聯歡晚會開幕前已排好有8個不同節目的節目單,如果保持原來的節目相對順序不變,臨時再插進去![]() 三個不同的新節目,且插進的三個新節目按
三個不同的新節目,且插進的三個新節目按![]() 順序出場,那么共有__________種不同的插入方法(用數字作答).
順序出場,那么共有__________種不同的插入方法(用數字作答).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:![]() )有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間
)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
![]()
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量![]() (單位:瓶)的分布列;
(單位:瓶)的分布列;
(2)設六月份一天銷售這種酸奶的利潤為![]() (單位:元),當六月份這種酸奶一天的進貨量
(單位:元),當六月份這種酸奶一天的進貨量![]() (單位:瓶)為多少時,
(單位:瓶)為多少時,![]() 的數學期望達到最大值?
的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+c,x∈[-2,2]表示過原點的曲線,且在x=±1處的切線的傾斜角均為![]() π,有以下命題:
π,有以下命題:
①f(x)的解析式為f(x)=x3-4x,x∈[-2,2].
②f(x)的極值點有且只有一個.
③f(x)的最大值與最小值之和等于零.
其中正確命題的序號為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求實數a的值;
(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某校為了解高一期末數學考試的情況,從高一的所有學生數學試卷中隨機抽取![]() 份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在
份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在![]() ,
,![]() 的學生人數為6.
的學生人數為6.
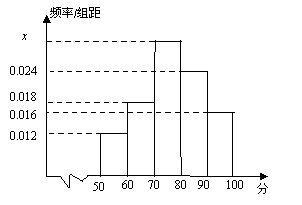
(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)試估計所抽取的數學成績的平均數;
(Ⅲ)試根據樣本估計“該校高一學生期末數學考試成績![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、F分別是橢圓C: ![]() +
+ ![]() =1(a>b>0)的左頂點、右焦點,點P為橢圓C上一動點,當PF⊥x軸時,AF=2PF.
=1(a>b>0)的左頂點、右焦點,點P為橢圓C上一動點,當PF⊥x軸時,AF=2PF.
(1)求橢圓C的離心率;
(2)若橢圓C存在點Q,使得四邊形AOPQ是平行四邊形(點P在第一象限),求直線AP與OQ的斜率之積;
(3)記圓O:x2+y2= ![]() 為橢圓C的“關聯圓”.若b=
為橢圓C的“關聯圓”.若b= ![]() ,過點P作橢圓C的“關聯圓”的兩條切線,切點為M、N,直線MN的橫、縱截距分別為m、n,求證:
,過點P作橢圓C的“關聯圓”的兩條切線,切點為M、N,直線MN的橫、縱截距分別為m、n,求證: ![]() +
+ ![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com