
【題目】已知![]() ,函數
,函數![]() ,
,![]() .
.
(1)若![]() 在
在![]() 上單調遞增,求正數
上單調遞增,求正數![]() 的最大值;
的最大值;
(2)若函數![]() 在
在![]() 內恰有一個零點,求
內恰有一個零點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)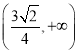
【解析】
(1)求出![]() 的單調遞增區間,令
的單調遞增區間,令![]() ,得
,得![]() ,可知區間
,可知區間![]()
![]() ,即可求出正數
,即可求出正數![]() 的最大值;(2)令
的最大值;(2)令![]() ,當
,當![]() 時,
時,![]() ,可將問題轉化為
,可將問題轉化為![]() 在
在![]() 的零點問題,分類討論即可求出答案.
的零點問題,分類討論即可求出答案.
解:(1)由![]() ,
,![]()
得![]() ,
,![]() .
.
因為![]() 在
在![]() 上單調遞增,
上單調遞增,
令![]() ,得
,得![]() 時
時![]() 單調遞增,
單調遞增,
所以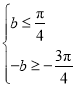 解得
解得![]() ,可得正數
,可得正數![]() 的最大值為
的最大值為![]() .
.
(2)![]()
![]() ,
,
設![]() ,當
,當![]() 時,
時,![]() .它的圖形如圖所示.
.它的圖形如圖所示.
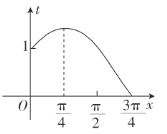
又![]() ,則
,則![]()
![]() ,
,![]() ,令
,令![]() ,
,
則函數![]() 在
在![]() 內恰有一個零點,可知
內恰有一個零點,可知![]() 在
在![]() 內最多一個零點.
內最多一個零點.
①當0為![]() 的零點時,
的零點時,![]() 顯然不成立;
顯然不成立;
②當![]() 為
為![]() 的零點時,由
的零點時,由![]() ,得
,得![]() ,把
,把![]() 代入
代入![]() 中,
中,
得![]() ,解得
,解得![]() ,
,![]() ,不符合題意.
,不符合題意.
③當零點在區間![]() 時,若
時,若![]() ,得
,得![]() ,此時零點為1,即
,此時零點為1,即![]() ,由
,由![]() 的圖象可知不符合題意;
的圖象可知不符合題意;
若![]() ,即
,即![]() ,設
,設![]() 的兩根分別為
的兩根分別為![]() ,
,![]() ,由
,由![]() ,且拋物線的對稱軸為
,且拋物線的對稱軸為![]() ,則兩根同時為正,要使
,則兩根同時為正,要使![]() 在
在![]() 內恰有一個零點,則一個根在
內恰有一個零點,則一個根在![]() 內,另一個根在
內,另一個根在![]() 內,
內,
所以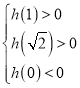 解得
解得![]() .
.
綜上,![]() 的取值范圍為
的取值范圍為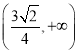 .
.


科目:高中數學 來源: 題型:
【題目】①回歸分析中,相關指數![]() 的值越大,說明殘差平方和越大;
的值越大,說明殘差平方和越大;
②對于相關系數![]() ,
,![]() 越接近1,相關程度越大,
越接近1,相關程度越大,![]() 越接近0,相關程度越小;
越接近0,相關程度越小;
③有一組樣本數據![]() 得到的回歸直線方程為
得到的回歸直線方程為![]() ,那么直線
,那么直線![]() 必經過點
必經過點![]() ;
;
④![]() 是用來判斷兩個分類變量是否有關系的隨機變量,只對于兩個分類變量適合;
是用來判斷兩個分類變量是否有關系的隨機變量,只對于兩個分類變量適合;
以上幾種說法正確的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,質量測試分為:指標不小于![]() 為一等品;指標不小于
為一等品;指標不小于![]() 且小于
且小于![]() 為二等品;指標小于
為二等品;指標小于![]() 為三等品。其中每件一等品可盈利
為三等品。其中每件一等品可盈利![]() 元,每件二等品可盈利
元,每件二等品可盈利![]() 元,每件三等品虧損
元,每件三等品虧損![]() 元。現對學徒甲和正式工人乙生產的產品各
元。現對學徒甲和正式工人乙生產的產品各![]() 件的檢測結果統計如下:
件的檢測結果統計如下:
測試指標 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
根據上表統計得到甲、乙生產產品等級的頻率分別估計為他們生產產品等級的概率。求:
(1)乙生產一件產品,盈利不小于![]() 元的概率;
元的概率;
(2)若甲、乙一天生產產品分別為![]() 件和
件和![]() 件,估計甲、乙兩人一天共為企業創收多少元?
件,估計甲、乙兩人一天共為企業創收多少元?
(3)從甲測試指標為![]() 與乙測試指標為
與乙測試指標為![]() 共
共![]() 件產品中選取
件產品中選取![]() 件,求兩件產品的測試指標差的絕對值大于
件,求兩件產品的測試指標差的絕對值大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的對邊分別為A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解該校學生對于某項運動的愛好是否與性別有關,通過隨機抽查110名學生,得到如下![]() 的列聯表:
的列聯表:
喜歡該項運動 | 不喜歡該項運動 | 總計 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
參照附表,以下結論正確的是( )
A. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
B. 在犯錯語的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
C. 有99%以上的把握認為“愛好該項運動與性別無關”
D. 有99%以上的把握認為“愛好該項運動與性別有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線E:x2=2py(p>0)的焦點F作斜率率分別為k1 , k2的兩條不同直線l1 , l2 , 且k1+k2=2.l1與E交于點A,B,l2與E交于C,D,以AB,CD為直徑的圓M,圓N(M,N為圓心)的公共弦所在直線記為l.
(1)若k1>0,k2>0,證明: ![]() ;
;
(2)若點M到直線l的距離的最小值為 ![]() ,求拋物線E的方程.
,求拋物線E的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com