【題目】在四棱錐P﹣ABCD中，PA⊥底面ABCD，底面ABCD為正方形，PA=AB，該四棱錐被一平面截去一部分后，剩余部分的三視圖如圖，則剩余部分體積與原四棱錐體積的比值為（ ）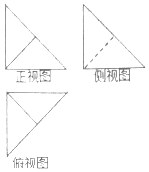
A.
B.
C.
D.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|cosx|sinx，給出下列五個說法： ①f（ 
π）=﹣ 
；
②若|f（x1）|=|f（x2）|，則x1=x2+kπ（k∈Z）；
③f（x）在區間[﹣ 
， ]上單調遞增；
④函數f（x）的周期為π．
⑤f（x）的圖象關于點（ 
，0）成中心對稱．
其中正確說法的序號是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
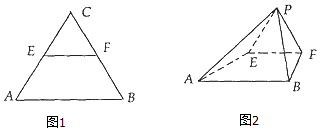
【題目】等腰△ABC中，AC=BC= 
，AB=2，E、F分別為AC、BC的中點，將△EFC沿EF折起，使得C到P，得到四棱錐P﹣ABFE，且AP=BP= 
． 
（1）求證：平面EFP⊥平面ABFE；
（2）求二面角B﹣AP﹣E的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖（1）所示，在直角梯形ABCD中， 
，E是AD的中點，O是AC與BE的交點．將△ABE沿BE折起到△A1BE的位置，如圖（2）所示．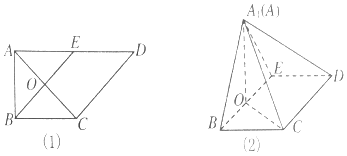 
（1）證明：CD⊥平面A1OC；
（2）若平面A1BE⊥平面BCDE，求平面A1BC與平面A1CD所成銳二面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數y=f（x）導函數的圖象如圖所示，則下列說法錯誤的是（ ）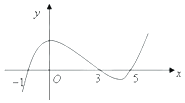
A.（﹣1，3）為函數y=f（x）的遞增區間
B.（3，5）為函數y=f（x）的遞減區間
C.函數y=f（x）在x=0處取得極大值
D.函數y=f（x）在x=5處取得極小值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知U=R，M={x|﹣l≤x≤2}，N={x|x≤3}，則（UM）∩N=（ ）
A.{x|2≤x≤3}
B.{x|2＜x≤3}
C.{x|x≤﹣1，或2≤x≤3}
D.{x|x＜﹣1，或2＜x≤3}
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列 
的前n項和為Sn 
，且滿足：
① 
；② 
，其中 
且 
．
（1）求p的值；
（2）數列 能否是等比數列？請說明理由；
（3）求證：當r 
2時，數列 是等差數列．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
