解:(1)由已知,橢圓方程可設為

.(1分)
∵兩個焦點和短軸的兩個端點恰為正方形的頂點,且短軸長為2,
∴
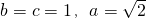
.
所求橢圓方程為

.(4分)
(2)右焦點F(1,0),直線l的方程為y=x-1.
設P(x
1,y
1),Q(x
2,y
2),
由
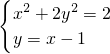
得3y
2+2y-1=0,解得

.
∴
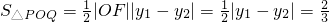
.(9分)
(3)假設在線段OF上存在點M(m,0)(0<m<1),使得以MP,MQ為鄰邊的平行四邊形是菱形.因為直線與x軸不垂直,所以設直線l的方程為y=k(x-1)(k≠0).
由

可得(1+2k
2)x
2-4k
2x+2k
2-2=0.
∴
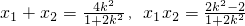
.
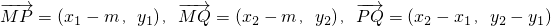
.其中x
2-x
1≠0
以MP,MQ為鄰邊的平行四邊形是菱形
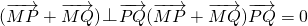
?(x
1+x
2-2m,y
1+y
2)(x
2-x
1,y
2-y
1)=0?(x
1+x
2-2m)(x
2-x
1)+(y
1+y
2)(y
2-y
1)=0?(x
1+x
2-2m)+k(y
1+y
2)=0
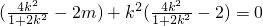
?2k
2-(2+4k
2)m=0
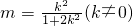
.
∴

.(14分)
分析:(1)設橢圓方程為

.由兩個焦點和短軸的兩個端點恰為正方形的頂點,且短軸長為2,由此能夠求出a,b,c的值,從而得到所求橢圓方程.
(2)右焦點F(1,0),直線l的方程為y=x-1.設P(x
1,y
1),Q(x
2,y
2),由題設條件得

.由此入手可求出
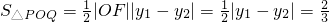
.
(3)假設在線段OF上存在點M(m,0)(0<m<1),使得以MP,MQ為鄰邊的平行四邊形是菱形.因為直線與x軸不垂直,設直線l的方程為y=k(x-1)(k≠0).由題意知(1+2k
2)x
2-4k
2x+2k
2-2=0.由此可知

.
點評:本題考查圓錐曲線的位置關系,解題時要認真審題,仔細解答.

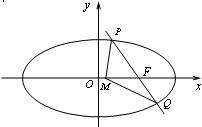 已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點.
已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點. .(1分)
.(1分)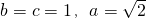 .
. .(4分)
.(4分)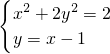 得3y2+2y-1=0,解得
得3y2+2y-1=0,解得 .
.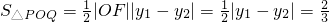 .(9分)
.(9分) 可得(1+2k2)x2-4k2x+2k2-2=0.
可得(1+2k2)x2-4k2x+2k2-2=0.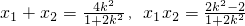 .
.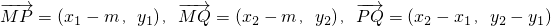 .其中x2-x1≠0
.其中x2-x1≠0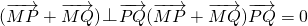 ?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0
?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0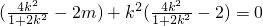 ?2k2-(2+4k2)m=0
?2k2-(2+4k2)m=0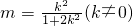 .
. .(14分)
.(14分) .由兩個焦點和短軸的兩個端點恰為正方形的頂點,且短軸長為2,由此能夠求出a,b,c的值,從而得到所求橢圓方程.
.由兩個焦點和短軸的兩個端點恰為正方形的頂點,且短軸長為2,由此能夠求出a,b,c的值,從而得到所求橢圓方程. .由此入手可求出
.由此入手可求出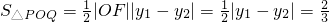 .
. .
.

 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案 已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點.
已知橢圓的中心在坐標原點O,焦點在x軸上,短軸長為2,且兩個焦點和短軸的兩個端點恰為一個正方形的頂點.過右焦點F與x軸不垂直的直線l交橢圓于P,Q兩點.