
【題目】已知二次函數f(x)=ax2+bx+c,(a,b,c∈R)滿足,對任意實數x,都有f(x)≥x,且當x∈(1,3)時,有f(x)≤ ![]() (x+2)2成立.
(x+2)2成立.
(1)證明:f(2)=2;
(2)若f(﹣2)=0,求f(x)的表達式;
(3)在(2)的條件下,設g(x)=f(x)﹣ ![]() x,x∈[0,+∞),若g(x)圖象上的點都位于直線y=
x,x∈[0,+∞),若g(x)圖象上的點都位于直線y= ![]() 的上方,求實數m的取值范圍.
的上方,求實數m的取值范圍.
【答案】
(1)解:由條件知:f(2)=4a+2b+c≥2成立,
又另取x=2時, ![]() 成立,
成立,
∴f(2)=2
(2)解:∵ 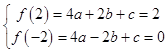 ,∴
,∴ ![]() ,4a+c=1,
,4a+c=1,
又f(x)≥x恒成立,即ax2+(b﹣1)x+c≥0在R上恒成立,
∴a>0且△=(b﹣1)2﹣4ac≤0, ![]() ,
,
解得: ![]() ,
,
所以 ![]()
(3)解:由題意可得:g(x)= ![]() +
+ ![]() 在[0,+∞)時必須恒成立,即x2+4(1﹣m)x+2>0在[0,+∞)時恒成立,
在[0,+∞)時必須恒成立,即x2+4(1﹣m)x+2>0在[0,+∞)時恒成立,
則有以下兩種情況:
①△<0,即16(1﹣m)2﹣8<0,解得 ![]()
② 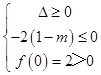 ,解得:
,解得: ![]() ,
,
綜上所述: 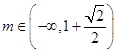
【解析】(1)由已知f(2)≥2成立,又由f(x))≤ ![]() (x+2)2成立,得f(2)≤
(x+2)2成立,得f(2)≤ ![]() =2,根據兩種情況可得f(2)值;f(﹣2)=0,由上述證明知f(2)=2,f(x)的表達式中有三個未知數,由兩函數值只能得出兩個方程,再對任意實數x,都有f(x)≥x,這一恒成立的關系得到
=2,根據兩種情況可得f(2)值;f(﹣2)=0,由上述證明知f(2)=2,f(x)的表達式中有三個未知數,由兩函數值只能得出兩個方程,再對任意實數x,都有f(x)≥x,這一恒成立的關系得到 ![]() 0,由此可以得到a=
0,由此可以得到a= ![]() ,將此三方程聯立可解出三個參數的值,求出f(x)的表達式;(3)g(x)=
,將此三方程聯立可解出三個參數的值,求出f(x)的表達式;(3)g(x)= ![]() +
+ ![]() 在[0,+∞)時必須恒成立,即x2+4(1﹣m)x+2>0在x∈[0,+∞)恒成立.轉化為二次函數圖象與x軸在x∈[0,+∞)無交點的問題,由于g(x)的單調性不確定,故本題要分兩種情況討論,一種是對稱軸在y軸右側,此時需要判別式小于0,一類是判別式大于0,對稱軸小于0,且x=0處的函數值大于等于0,轉化出相應的不等式求解.
在[0,+∞)時必須恒成立,即x2+4(1﹣m)x+2>0在x∈[0,+∞)恒成立.轉化為二次函數圖象與x軸在x∈[0,+∞)無交點的問題,由于g(x)的單調性不確定,故本題要分兩種情況討論,一種是對稱軸在y軸右側,此時需要判別式小于0,一類是判別式大于0,對稱軸小于0,且x=0處的函數值大于等于0,轉化出相應的不等式求解.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知 ![]() 是定義在(﹣∞,+∞)上的奇函數,且滿足
是定義在(﹣∞,+∞)上的奇函數,且滿足 ![]()
(1)求實數a,b,并確定函數f(x)的解析式
(2)用定義證明f(x)在(﹣1,1)上是增函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: (![]() >b>0)的離心率為
>b>0)的離心率為![]() ,A(
,A(![]() ,0), B(0,b),O(0,0),△OAB的面積為1.
,0), B(0,b),O(0,0),△OAB的面積為1.
(1)求橢圓C的方程;
(2)設P是橢圓C上一點,直線PA與y軸交于點M,直線PB與x軸交于點N.求證:|AN|·|BM|為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:(x+1)(x﹣5)≤0,命題q:1﹣m≤x<1+m(m>0).
(1)若p是q的充分條件,求實數m的取值范圍;
(2)若m=5,“p∨q”為真命題,“p∧q”為假命題,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.現已畫出函數f(x)在y軸左側的圖象,如圖所示,并根據 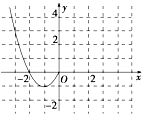
(1)寫出函數f(x)(x∈R)的增區間;
(2)寫出函數f(x)(x∈R)的解析式;
(3)若函數g(x)=f(x)﹣2ax+2(x∈[1,2]),求函數g(x)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,且當x≤0時,f(x)=x2+2x.現已畫出函數f(x)在y軸左側的圖象,如圖所示,根據圖象: 
(1)寫出函數f(x),x∈R的增區間并將圖象補充完整;
(2)寫出函數f(x),x∈R的解析式;
(3)若函數g(x)=f(x)﹣4ax+2,x∈[1,3],求函數g(x)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲乙兩船,其中甲船在某島B的正南方A處,A與B相距7公里,甲船自A處以4公里/小時的速度向北方向航行,同時乙船以6公里/小時的速度自B島出發,向北60°西方向航行,問分鐘后兩船相距最近.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com