解:由y=xcosx,得到y′=cosx-xsinx,
把x=

代入導函數得:y′

=-

,即切線方程的斜率k=-

,
把x=

代入曲線方程得:y=0,則切點坐標為(

,0),
所以切線方程為:y=-

(x-

),即2πx+4y-π
2=0.
分析:根據曲線方程的解析式,求出導函數,把x=

代入導函數中求出的導函數值即為切線方程的斜率,把x=

代入函數解析式中求出的函數值即為切點的縱坐標,進而得到切點的坐標,由求出的斜率和切點坐標寫出切線方程即可.
點評:此題考查學生會利用導數求曲線上過某點切線方程的斜率,會根據一點坐標和斜率寫出直線的方程,是一道基礎題.

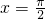 處的切線方程.
處的切線方程.