
【題目】已知函數![]() (
(![]() 是非零實常數)滿足
是非零實常數)滿足![]() 且方程
且方程![]() 有且僅有一個實數解.
有且僅有一個實數解.
(1)求![]() 的值
的值
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍
的取值范圍
(3)在直角坐標系中,求定點![]() 到函數
到函數![]() 圖像上的任意一點
圖像上的任意一點![]() 的距離
的距離![]() 的最小值,并求取得最小值時
的最小值,并求取得最小值時![]() 的值
的值
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論錯誤的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30萬人
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司在某市的貨物轉運中心,擬引進智能機器人分揀系統,以提高分揀效率和降低物流成本,已知購買x臺機器人的總成本為![]() 萬元.
萬元.

(1)若使每臺機器人的平均成本最低,問應買多少臺?
(2)現按(1)中的數量購買機器人,需要安排m人將郵件放在機器人上,機器人將郵件送達指定落袋格口完成分揀(如圖).經實驗知,每臺機器人的日平均分揀量為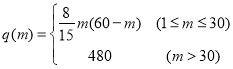 ,(單位:件).已知傳統的人工分揀每人每日的平均分揀量為1200件,問引進機器人后,日平均分揀量達最大時,用人數量比引進機器人前的用人數量最多可減少百分之幾?
,(單位:件).已知傳統的人工分揀每人每日的平均分揀量為1200件,問引進機器人后,日平均分揀量達最大時,用人數量比引進機器人前的用人數量最多可減少百分之幾?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 是一個歷史文物展覽廳的俯視圖,點
是一個歷史文物展覽廳的俯視圖,點![]() 在
在![]() 上,在梯形
上,在梯形![]() 區域內部展示文物,
區域內部展示文物,![]() 是玻璃幕墻,游客只能在
是玻璃幕墻,游客只能在![]() 區域內參觀.在
區域內參觀.在![]() 上點
上點![]() 處安裝一可旋轉的監控攝像頭.
處安裝一可旋轉的監控攝像頭.![]() 為監控角,其中
為監控角,其中![]() 、
、![]() 在線段
在線段![]() (含端點)上,且點
(含端點)上,且點![]() 在點
在點![]() 的右下方.經測量得知:
的右下方.經測量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .記
.記![]() (弧度),監控攝像頭的可視區域
(弧度),監控攝像頭的可視區域![]() 的面積為
的面積為![]() 平方米.
平方米.

(1)求![]() 關于
關于![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍;(參考數據:
的取值范圍;(參考數據:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 經過點
經過點![]() ,
,![]() ,點
,點![]() 為橢圓
為橢圓![]() 的右頂點,直線
的右頂點,直線![]() 與橢圓相交于不同于點
與橢圓相交于不同于點![]() 的兩個點
的兩個點![]() 、
、![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)當![]() 時,求
時,求![]() 面積的最大值;
面積的最大值;
(3)若![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某游戲棋盤上標有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子開始位于第
站,棋子開始位于第![]() 站,選手拋擲均勻硬幣進行游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到跳到第
站,選手拋擲均勻硬幣進行游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到跳到第![]() 站或第
站或第![]() 站時,游戲結束.設游戲過程中棋子出現在第
站時,游戲結束.設游戲過程中棋子出現在第![]() 站的概率為
站的概率為![]() .
.
(1)當游戲開始時,若拋擲均勻硬幣![]() 次后,求棋子所走站數之和
次后,求棋子所走站數之和![]() 的分布列與數學期望;
的分布列與數學期望;
(2)證明:![]() ;
;
(3)若最終棋子落在第![]() 站,則記選手落敗,若最終棋子落在第
站,則記選手落敗,若最終棋子落在第![]() 站,則記選手獲勝.請分析這個游戲是否公平.
站,則記選手獲勝.請分析這個游戲是否公平.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)若對任意的![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() 的最小值為
的最小值為![]() ,求實數
,求實數![]() 的值;
的值;
(3)若對任意實數![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 為三邊邊長的三角形,求實數
為三邊邊長的三角形,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:極坐標與參數方程
已知在平面直角坐標系xOy中,O為坐標原點,曲線C: 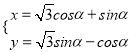 (α為參數),在以平面直角坐標系的原點為極點,x軸的正半軸為極軸,取相同單位長度的極坐標系,直線l:ρ
(α為參數),在以平面直角坐標系的原點為極點,x軸的正半軸為極軸,取相同單位長度的極坐標系,直線l:ρ![]() .
.
(Ⅰ)求曲線C的普通方程和直線l的直角坐標方程;
(Ⅱ)曲線C上恰好存在三個不同的點到直線l的距離相等,分別求出這三個點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果存在常數a,使得數列{an}滿足:若x是數列{an}中的一項,則a-x也是數列{an}中的一項,稱數列{an}為“兌換數列”,常數a是它的“兌換系數”.
(1)若數列:2,3,6,m(m>6)是“兌換系數”為a的“兌換數列”,求m和a的值;
(2)已知有窮等差數列{bn}的項數是n0(n0≥3),所有項之和是B,求證:數列{bn}是“兌換數列”,并用n0和B表示它的“兌換系數”;
(3)對于一個不少于3項,且各項皆為正整數的遞增數列{cn},是否有可能它既是等比數列,又是“兌換數列”?給出你的結論,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com