
已知函數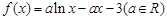 .(I)當
.(I)當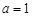 時,求函數
時,求函數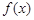 的單調區間;(II)若函數
的單調區間;(II)若函數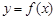 的圖象在點
的圖象在點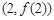 處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的
處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的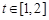 ,函數
,函數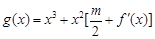 在區間
在區間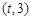 上總存在極值?
上總存在極值?
(1)在(0,1)上單調遞增;在(1,+∞)上單調遞減. (2)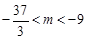
【解析】本試題主要考查了導數在研究函數中的運用。通過a的值可知,函數解析式,求解導數,然后令導數大于零和導數小于零,得到單調區間。并利用導數的幾何意義得到切線的斜率等的運用。、
(1)直接求解導數,然后解導數的不等式得到單調增減區間。
(2)利用對于任意的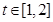 ,函數y=g(x)在區間
,函數y=g(x)在區間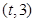 上總存在極值,轉化為
上總存在極值,轉化為
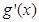 在x=2,x=3處的導數值分別為小于零和大于零得到參數m的取值范圍。
在x=2,x=3處的導數值分別為小于零和大于零得到參數m的取值范圍。
解: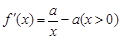
(I)當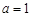 時,
時,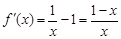 ,
…………………………………2分
,
…………………………………2分
令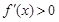 時,解得
時,解得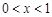 ,所以
,所以 在(0,1)上單調遞增; ……4分
在(0,1)上單調遞增; ……4分
令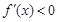 時,解得
時,解得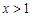 ,所以
,所以 在(1,+∞)上單調遞減.
………6分
在(1,+∞)上單調遞減.
………6分
(II)因為函數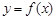 的圖象在點(2,
的圖象在點(2,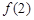 )處的切線的傾斜角為45o,
)處的切線的傾斜角為45o,
所以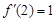 .
.
所以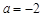 ,
,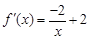 . ………………………………………………8分
. ………………………………………………8分

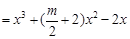 ,
,
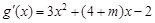 , ……………………………………………10分
, ……………………………………………10分
因為任意的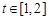 ,函數
,函數 在區間
在區間 上總存在極值,
上總存在極值,
所以只需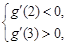 ……………………………………………………12分
……………………………………………………12分
解得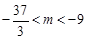 .
.


科目:高中數學 來源:2014屆海南瓊海嘉積中學高二上教學監測(三)文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)
已知函數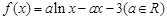 .
.
(I)當 時,求函數
時,求函數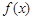 的單調區間;
的單調區間;
(II)若函數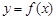 的圖象在點
的圖象在點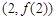 處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的
處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的 ,函數
,函數 在區間
在區間 上總存在極值?
上總存在極值?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北省八市高三三月聯考文科數學 題型:解答題
(本小題滿分14分)
已知函數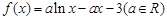 .
.
(I)當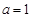 時,求函數
時,求函數 的單調區間;
的單調區間;
(II)若函數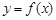 的圖象在點
的圖象在點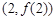 處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的
處的切線的傾斜角為45o,問:m在什么范圍取值時,對于任意的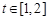 ,函數
,函數 在區間
在區間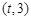 上總存在極值?
上總存在極值?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年丹東市四校協作體高三摸底測試數學文(零診) 題型:解答題
(本小題滿分12分)已知函數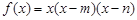 .
.
(I)當 時,若函數
時,若函數 在
在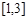 上單調遞減,求實數
上單調遞減,求實數 的取值范圍;
的取值范圍;
(II)若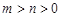 ,
,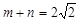 ,且過原點存在兩條互相垂直的直線與曲線
,且過原點存在兩條互相垂直的直線與曲線 均相切,求
均相切,求 和
和 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:北京市西城區09-10學年高二下學期期末數學試題(文科) 題型:解答題
(本小題滿分14分)
已知函數 .
.
(I)當 時,求曲線
時,求曲線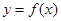 在點
在點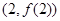 處切線的斜率;
處切線的斜率;
(II)當 時,求函數
時,求函數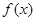 的單調區間.
的單調區間.
查看答案和解析>>
科目:高中數學 來源:2010年北京市海淀區高三第二次模擬考試數學(文) 題型:解答題
(本小題滿分14分)
已知函數 ,
,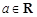
(I)當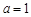 時,求函數
時,求函數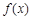 的極值;
的極值;
(II)若函數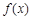 在區間
在區間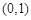 上是單調增函數,求實數
上是單調增函數,求實數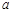 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com