分析:(1)觀察集合關系,由于兩集合相等,發現其對應特征,建立方程求出a,b的值
(2)將a,b的值代入,先判斷單調性,再用定義法證明即可.
解答:解:(1)兩集合相等,觀察發現a不能為O,故只有b
2-1=0,得b=-1,或b=1
當b=-1時,故b與a對應,所以a=-1,
如果b=1則必有|a|=1,B不成立;
故a=-1,b=-1…4分
(2)由(1)得
f(x)= x+,因為x∈R時,當x>0時,
f(x)= x+≥2,x=1時取得最小值,
函數
f(x)= x+的單調增區間為(-∞,-1],[1,+∞);函數是奇函數,單調減區間為:(-1,0),(0,1).
①在[1,+∞)是增函數
任取x
1,x
2∈[1,+∞)令x
1<x
2,
f(x
1)-f(x
2)=
x1+-
x2-=(x
1-x
2)(1-
)
∵1≤x
1<x
2,
∴x
1-x
2<0,又x
1x
2>1,故1-
>0
∴f(x
1)-f(x
2)=(x
1-x
2)(1-
)<0
∴f(x
1)<f(x
2)
故
f(x)= x+,在[1,+∞)是增函數.
因為函數
f(x)= x+是奇函數,所以(-∞,-1]也是增函數;…8分
②函數在x∈(0,1)時,
任取x
1,x
2∈(0,1),令x
1<x
2,
f(x
1)-f(x
2)=
x1+-
x2-=(x
1-x
2)(1-
)
∵0<x
1<x
2<1
∴x
1-x
2<0,又1>x
1x
2>0,故1-
<0
∴f(x
1)-f(x
2)=(x
1-x
2)(1-
)>0
∴f(x
1)>f(x
2)
故
f(x)= x+,在(0,1)是減函數.
因為函數
f(x)= x+是奇函數,所以(-1,0)也是減函數.
綜上函數
f(x)= x+的單調增區間為(-∞,-1],[1,+∞);
單調減區間為:(-1,0),(0,1).…12分
點評:本題考查集合相等的概念以及函數單調性的證明方法--定義法,解答第二小問時要注意步驟,先判斷再證明,注意分類討論思想的應用.



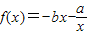 在[1,+∞)的單調性,并用定義加以證明.
在[1,+∞)的單調性,并用定義加以證明.