【題目】已知三棱錐
的所有頂點都在球
的球面上，
平面
，
，
，若球的表面積為
，則三棱錐的側面積的最大值為（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由題意畫出圖形，設球O得半徑為R，AB=x，AC=y，由球O的表面積為29π，可得x2+y2=25，寫出側面積，再由基本不等式求最值．
設球O得半徑為R，AB=x，AC=y，
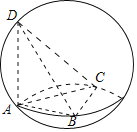
由4πR2=29π，得4R2=29．又x2+y2+22=（2R）2，得x2+y2=25．三棱錐A-BCD的側面積：S=S△ABD+S△ACD+S△ABC=
由x2+y2≥2xy，得xy≤
當且僅當x=y=
時取等號，由（x+y）2=x2+2xy+y2≤2（x2+y2），得x+y≤5
,當且僅當x=y=時取等號，∴S≤5+
=
當且僅當x=y=時取等號. ∴三棱錐A-BCD的側面積的最大值為.故選A.
科目：高中數學 來源： 題型：
【題目】某日A, B, C三個城市18個銷售點的小麥價格如下表：
銷售點序號 | 所屬城市 | 小麥價格（元/噸） | 銷售點序號 | 所屬城市 | 小麥價格（元/噸） |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
（Ⅰ）求B市5個銷售點小麥價格的中位數；
（Ⅱ）甲從B市的銷售點中隨機挑選一個購買1噸小麥，乙從C市的銷售點中隨機挑選一個購買1噸小麥，求甲花費的費用比乙高的概率；
（Ⅲ）如果一個城市的銷售點小麥價格方差越大，則稱其價格差異性越大.請你對A、B、C三個城市按照小麥價格差異性從大到小進行排序（只寫出結果）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的最小正周期為
，將函數
的圖像向右平移
個單位長度，再向下平移
個單位長度，得到函數
的圖像.
（1）求函數的單調遞增區間；
（2）在銳角
中，角
的對邊分別為
，若
，
，求面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過橢圓W:
的左焦點
作直線
交橢圓于
兩點，其中
，另一條過的直線
交橢圓于
兩點（不與重合），且
點不與點
重合.過作
軸的垂線分別交直線
，
于
,
.
（Ⅰ）求
點坐標和直線的方程；
（Ⅱ）求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
，
，數列
滿足條件:對于
，
，且
，并有關系式:
，又設數列
滿足
(
且
，).
（1）求證數列
為等比數列，并求數列的通項公式；
（2）試問數列
是否為等差數列，如果是，請寫出公差，如果不是，說明理由；
（3）若
，記
，，設數列
的前
項和為
，數列的前項和為
，若對任意的，不等式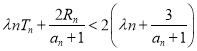
恒成立，試求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校200名學生的數學期中考試成績頻率分布直方圖如圖所示，其中成績分組區間是
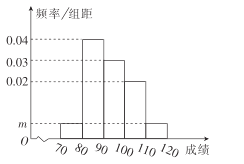
（1）求圖中
的值；
（2）根據頻率分布直方圖，估計這200名學生的平均分；
（3）若這200名學生的數學成績中，某些分數段的人數
與英語成績相應分數段的人數
之比如表所示，求英語成績在
的人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列命題：
①回歸直線
恒過樣本點的中心
，且至少過一個樣本點；
②兩個變量相關性越強，則相關系數r就越接近于1；
③將一組數據的每個數據都加一個相同的常數后，方差不變；
④在回歸直線方程
中，當解釋變量x增加一個單位時，預報變量
平均減少0.5；
⑤在線性回歸模型中，相關指數
表示解釋變量
對于預報變量
的貢獻率，越接近于1，表示回歸效果越好；
⑥對分類變量
與
，它們的隨機變量
的觀測值
來說， 越小，“與有關系”的把握程度越大．
⑦兩個模型中殘差平方和越小的模型擬合的效果越好.
則正確命題的個數是（ ）
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
