
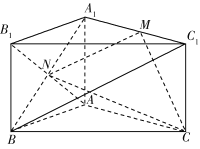
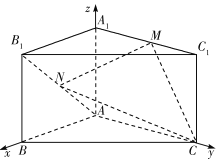
【題目】【2018海南高三階段性測試(二模)】如圖,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 上一動點.
上一動點.

(I)是否存在一點![]() ,使得線段
,使得線段![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
(II)若點![]() 為
為![]() 的中點且
的中點且![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(I)見解析(II)![]()
【解析】試題分析:
(1)存在點![]() ,且
,且![]() 為
為![]() 的中點.連接
的中點.連接![]() ,
, ![]() ,由三角形中位線的性質可得
,由三角形中位線的性質可得![]() ,結合線面平行的判定定理可得
,結合線面平行的判定定理可得![]() 平面
平面![]() .
.
(2)由題意結合勾股定理可求得![]() .以點
.以點![]() 為坐標原點,
為坐標原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸建立空間直角坐標系,可得平面
軸建立空間直角坐標系,可得平面![]() 的一個法向量為
的一個法向量為![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]() ,據此計算可得二面角
,據此計算可得二面角![]() 的正弦值為
的正弦值為![]() .
.
試題解析:
(1)存在點![]() ,且
,且![]() 為
為![]() 的中點.證明如下:
的中點.證明如下:
如圖,連接![]() ,
, ![]() ,點
,點![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,
的中點,
所以![]() 為
為![]() 的一條中位線,
的一條中位線, ![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)設![]() ,則
,則![]() ,
, ![]()
![]()
![]()
![]() ,
,
![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() .
.
由題意以點![]() 為坐標原點,
為坐標原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸建立如圖所示的空間直角坐標系,可得
軸建立如圖所示的空間直角坐標系,可得![]() ,
, ![]() ,
, 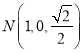 ,
, ![]() ,
,
故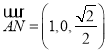 ,
, ![]() ,
, 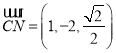 ,
, ![]() .
.
設![]() 為平面
為平面![]() 的一個法向量,則
的一個法向量,則
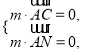 得
得
令![]() ,得平面
,得平面![]() 的一個法向量
的一個法向量![]() ,
,
同理可得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
故二面角![]() 的余弦值為
的余弦值為![]()
![]() .
.
故二面角![]() 的正弦值為
的正弦值為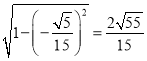 .
.


科目:高中數學 來源: 題型:
【題目】已知冪函數![]() ,滿足
,滿足![]() .
.
(![]() )求函數
)求函數![]() 的解析式.
的解析式.
(![]() )若函數
)若函數![]() ,
,![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 的最小值為
的最小值為![]() ?
?
若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(![]() )若函數
)若函數![]() ,是否存在實數
,是否存在實數![]() ,
,![]() ,使函數
,使函數![]() 在
在![]() 上的值域為
上的值域為![]() ?若存在,求出實數
?若存在,求出實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取M名學生作為樣本,得到這M名學生參加社區服務的次數,根據此數據作出了頻數與頻率的統計表和頻率分布直方圖.
分組 | 頻數 | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合計 | M | 1 |

(1)求出表中M,p及圖中a的值;
(2)若該校高三學生有240人,試估計該校高三學生參加社區服務的次數在區間[10,15)內的人數;
(3)估計這次學生參加社區服務人數的眾數、中位數以及平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在每年的春節后,某市政府都會發動公務員參與到植樹綠化活動中去.林業管理部門在植樹前,為了保證樹苗的質量,都會在植樹前對樹苗進行檢測.現從甲、乙兩種樹苗中各抽測了10株樹苗,量出它們的高度如下(單位:厘米):
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)畫出兩組數據的莖葉圖,并根據莖葉圖對甲、乙兩種樹苗的高度作比較,寫出兩個統計結論;
(2)設抽測的10株甲種樹苗高度平均值為![]() ,將這10株樹苗的高度依次輸入,按程序框(如圖)進行運算,問輸出的S大小為多少?并說明S的統計學意義.
,將這10株樹苗的高度依次輸入,按程序框(如圖)進行運算,問輸出的S大小為多少?并說明S的統計學意義.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中, ![]() ,
, ![]() 與
與![]() 交于
交于![]() 點,現將
點,現將![]() 沿
沿![]() 折起得到三棱錐
折起得到三棱錐![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.

(1)求證: ![]() ;
;
(2)若三棱錐![]() 的最大體積為
的最大體積為![]() ,當三棱錐
,當三棱錐![]() 的體積為
的體積為![]() ,且
,且![]() 為銳角時,求三棱錐
為銳角時,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣0.5x+1,則不等式f(2x﹣3)<0.5的解集為( )
A.{x|﹣1<x<1.5}
B.{x|0.5<x<2}
C.{x|x<2}
D.{x|1.5<x<2}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.命題“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1<0
B.命題“若x=3,則x2﹣2x﹣3=0”的否命題是:若x≠3,則x2﹣2x﹣3≠0
C.“ ![]() ”是“
”是“ ![]() ”的必要而不充分條件
”的必要而不充分條件
D.命題“cosx=cosy,則x=y”的逆否命題是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的兩個焦點是F1(﹣2,0),F2(2,0),且橢圓C經過點A(0, ![]() ).
).
(1)求橢圓C的標準方程;
(2)若過橢圓C的左焦點F1(﹣2,0)且斜率為1的直線l與橢圓C交于P、Q兩點,求線段PQ的長(提示:|PQ|= ![]() |x1﹣x2|).
|x1﹣x2|).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com