
橢圓 的長軸長為4,焦距為2,F1、F2分別為橢圓的左、右焦點,直線
的長軸長為4,焦距為2,F1、F2分別為橢圓的左、右焦點,直線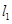 過點
過點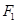 且垂直于橢圓的長軸,動直線
且垂直于橢圓的長軸,動直線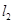 垂直
垂直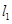 于點
于點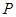 ,線段
,線段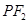 垂直平分線交
垂直平分線交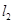 于點
于點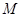
(1)求橢圓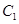 的標準方程和動點
的標準方程和動點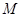 的軌跡
的軌跡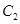 的方程。
的方程。
(2)過橢圓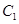 的右焦點
的右焦點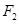 作斜率為1的直線交橢圓于A、B兩點,求
作斜率為1的直線交橢圓于A、B兩點,求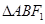 的面積。
的面積。
(3)設軌跡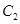 與
與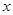 軸交于點
軸交于點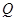 ,不同的兩點
,不同的兩點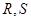 在軌跡
在軌跡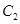 上,
上,
滿足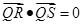 求證:直線
求證:直線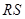 恒過
恒過 軸上的定點。
軸上的定點。
解:(1)由題設知:2a = 4,即a = 2,2c=2,即c=1,
故橢圓方程為 , ………2分
, ………2分
∵MP=MF2,
∴動點M到定直線 的距離等于它到定點F1(1,0)的距離,
的距離等于它到定點F1(1,0)的距離,
∴動點M的軌跡是C為l1準線,F2為焦點的拋物線
∴點M的軌跡C2的方程為  …………5分
…………5分
(2) 消去
消去 并整理得:
并整理得:
設
 則
則  ---------------7分
---------------7分
 =
= -----------9分
-----------9分
(3)Q(0,0),設
 ------------10分
------------10分




 ---------------------------11分
---------------------------11分






 ----------------13 分
----------------13 分
故直線RS恒過定點(4,0)-------------------------------------------------------14分
【解析】略


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
 (文科做)已知點A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b為正常數.
(文科做)已知點A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b為正常數.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 (文科做)已知點A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b為正常數.
(文科做)已知點A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b為正常數.查看答案和解析>>
科目:高中數學 來源:2010年湖北省高考數學模擬試卷(文理合卷)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com