已知數(shù)列

的前

項和為

,

.
(Ⅰ)求數(shù)列

的通項公式;
(Ⅱ)設

,求數(shù)列

的前

項和

.
(Ⅰ)

;(Ⅱ)

.
試題分析:(Ⅰ)由
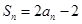
,求數(shù)列

的通項公式,可利用

來求,注意需討論

時的情況,本題由

,得到數(shù)列

的遞推式,從而得數(shù)列

為等比數(shù)列,利用等比數(shù)列的通項公式可得,

;(Ⅱ)求數(shù)列

的前

項和

,需求出數(shù)列

的通項公式,

,這是一個等比數(shù)列與一個等差數(shù)列對應項積所組成的數(shù)列,故可用錯位相減法來求.
試題解析:(Ⅰ)當

時,

, 1分
當

時,

3分
即:

,

數(shù)列

為以2為公比的等比數(shù)列 5分

7分
(Ⅱ)

9分

11分
兩式相減,得

13分

14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列

的前

項和為

,且

,

,數(shù)列

滿足

,

.
(1)求

,

;
(2)求數(shù)列

的前

項和

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
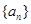
中,
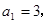
前
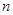
和
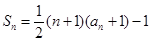
(1)求證:數(shù)列
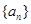
是等差數(shù)列
(2)求數(shù)列
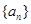
的通項公式
(3)設數(shù)列
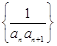
的前
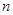
項和為
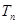
,是否存在實數(shù)
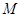
,使得
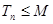
對一切正整數(shù)
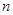
都成立?若存在,求
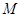
的最小值,若不存在,試說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
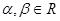
且
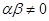
,數(shù)列
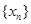
滿足
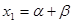
,
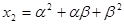
,
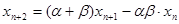
(
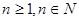
),令
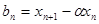
,
⑴求證:
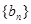
是等比數(shù)列;
⑵求數(shù)列
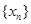
的通項公式;
⑶若
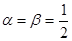
,求
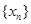
的前
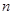
項和
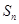
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
數(shù)列{an}滿足an+1+(-1)n an=2n-1,則{an}的前60項和為____________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
各項都為正數(shù)的數(shù)列
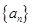
,其前
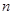
項的和為
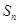
,且
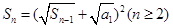
,若
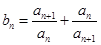
,且數(shù)列
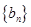
的前
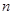
項的和為
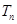
,則
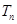
=
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
數(shù)列
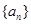
的通項公式為
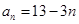
,
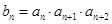
,
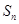
是數(shù)列
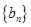
的前
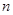
項和,則
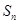
的最大值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知等差數(shù)列

的通項公式為

,設

,則當
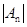
取得最小值是,n的值是 ( )
查看答案和解析>>

 的前
的前 項和為
項和為 ,
, .
. 的通項公式;
的通項公式; ,求數(shù)列
,求數(shù)列 的前
的前 項和
項和 .
. 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案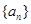 中,
中,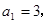 前
前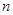 和
和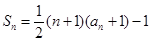
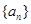 是等差數(shù)列
是等差數(shù)列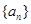 的通項公式
的通項公式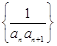 的前
的前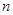 項和為
項和為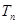 ,是否存在實數(shù)
,是否存在實數(shù)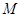 ,使得
,使得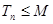 對一切正整數(shù)
對一切正整數(shù)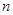 都成立?若存在,求
都成立?若存在,求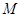 的最小值,若不存在,試說明理由。
的最小值,若不存在,試說明理由。 的前n項和
的前n項和 ,則( )
,則( ) 是遞增的等比數(shù)列
是遞增的等比數(shù)列 是遞增數(shù)列,但不是等比數(shù)列
是遞增數(shù)列,但不是等比數(shù)列 是遞減的等比數(shù)列
是遞減的等比數(shù)列 不是等比數(shù)列,也不單調(diào)
不是等比數(shù)列,也不單調(diào)