
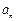 逐月遞增且控制在2萬件內;
逐月遞增且控制在2萬件內;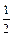 an2 (n∈N*)
an2 (n∈N*)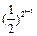
 ①
①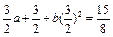 ②
②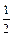 從而an + 1 =" 2an" –
從而an + 1 =" 2an" –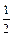 an2 (n∈N*) ………………………5分
an2 (n∈N*) ………………………5分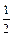 an2 = –
an2 = –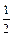 (an – 2)2 + 2≤2.
(an – 2)2 + 2≤2.  <2
<2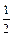 an2 + 2an – an = –
an2 + 2an – an = –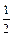 an (an – 2) >0,
an (an – 2) >0,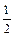 x2 + 2x = –
x2 + 2x = –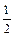 (x – 2)2 + 2在[0,2]上為增函數,
(x – 2)2 + 2在[0,2]上為增函數,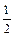 ak (4 – ak) <
ak (4 – ak) <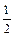 ak + 1(4 –ak + 1) <
ak + 1(4 –ak + 1) <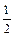 ×2×(4 – 2)
×2×(4 – 2) 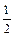 an2得2 (an + 1– 2) =" –" (an – 2)2 即(2 – an + 1) =
an2得2 (an + 1– 2) =" –" (an – 2)2 即(2 – an + 1) = 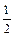 (2 – an)2
(2 – an)2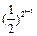 (n∈N*)為所求………13分
(n∈N*)為所求………13分

 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案科目:高中數學 來源:不詳 題型:解答題
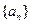 的通項公式為
的通項公式為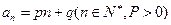 . 數列
. 數列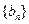 定義如下:對于正整數m,
定義如下:對于正整數m,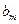 是使得不等式
是使得不等式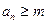 成立的所有n中的最小值.
成立的所有n中的最小值.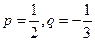 ,求
,求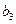 ;
;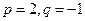 ,求數列
,求數列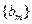 的前2m項和公式;
的前2m項和公式;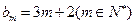 ?如果存在,求p和q的取值范圍;如果不存在,請說明理由.
?如果存在,求p和q的取值范圍;如果不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
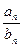 }的前n項和Sn;
}的前n項和Sn;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com