
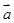 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),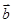 =(-
=(- ,
, ).
).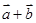 與
與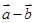 垂直;
垂直;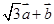 與
與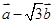 的模相等時,求角α.
的模相等時,求角α.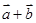 與
與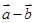 垂直,則利用數量積為零即可。
垂直,則利用數量積為零即可。 a+b|=|a-
a+b|=|a- b|,利用模相等,則平方后相等來解得關于角α的方程,然后解三角方程得到角的值。
b|,利用模相等,則平方后相等來解得關于角α的方程,然后解三角方程得到角的值。 ,sinα+
,sinα+ )·(cosα+
)·(cosα+ ,sinα-
,sinα- )
) )(cosα+
)(cosα+ )+(sinα+
)+(sinα+ )(sinα-
)(sinα- )
)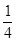 +sin2α-
+sin2α-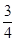 =0,
=0, a+b|=|a-
a+b|=|a- b|,平方得(
b|,平方得( a+b)2=(a-
a+b)2=(a- b)2,
b)2, ab=0①.
ab=0①. ,
, )=-
)=- cosα+
cosα+ sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:填空題
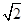 sinB-cosC的取值范圍為___________.
sinB-cosC的取值范圍為___________.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com