
【題目】一個透明密閉的正方體容器中,恰好盛有該容器一半容積的水,任意轉動這個正方體,則水面在容器中的形狀可以是:
①三角形;②矩形;③正方形;④正六邊形.
其中正確的結論是(把你認為正確的序號都填上)
【答案】②③④
【解析】解:∵正方體容器中盛有一半容積的水,無論怎樣轉動,其水面總是過正方體的中心.
于是過正方體的一條棱和中心可作一截面,截面形狀為長方形或矩形,如圖(1),所以③正確;
過正方體一面上一邊的中點和此邊外的頂點以及正方體的中心作一截面,其截面形狀為菱形,如圖(2);
過正方體一面上相鄰兩邊的中點以及正方體的中心作一截面,得截面形狀為正六邊形,如圖(3);,所以④正確;
正方體一面上相對兩邊的中點以及正方體的中心作一截面,得截面形狀為正方形,如圖(4),所以③正確.
所以答案是:②③④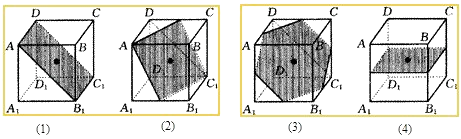
【考點精析】利用簡單空間圖形的三視圖對題目進行判斷即可得到答案,需要熟知畫三視圖的原則:長對齊、高對齊、寬相等.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某市在對高三學生的4月理科數學調研測試的數據統計顯示,全市10000名學生的成績服從正態分布![]() ,現從甲校100分以上(含100分)的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:
,現從甲校100分以上(含100分)的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:

(注:表中試卷編號![]() )
)
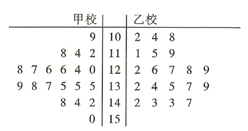
(1)列出表中試卷得分為126分的試卷編號(寫出具體數據);
(2)該市又從乙校中也用系統抽樣的方法抽取了20份試卷,將甲乙兩校這40份試卷的得分制作了莖葉圖(如圖6),試通過莖葉圖比較兩校學生成績的平均分及分散程度(均不要求計算出具體值,給出結論即可);
(3)在第(2)問的前提下,從甲乙兩校這40名學生中,從成績在140分以上(含140分)的學生中任意抽取3人,該3人在全市前15名的人數記為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
(附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列向量組中,能作為表示它們所在平面內所有向量的一組基底的是( )
A.![]() =(0,0)
=(0,0) ![]() =(1,﹣2)
=(1,﹣2)
B.![]() =(﹣1,2)
=(﹣1,2) ![]() =(3,7)
=(3,7)
C.![]() =(3,5)
=(3,5) ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3)
=(2,﹣3) ![]() =(
=( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知直線2x+y﹣8=0與直線x﹣2y+1=0交于點P.
(1)求過點P且平行于直線4x﹣3y﹣7=0的直線11的方程;(結果都寫成一般方程形式)
(2)求過點P的所有直線中使原點O到此直線的距離最大的直線12的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(ex , lnx+k),
=(ex , lnx+k), ![]() =(1,f(x)),
=(1,f(x)), ![]() ∥
∥ ![]() (k為常數,e是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與y軸垂直,F(x)=xexf′(x).
(k為常數,e是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與y軸垂直,F(x)=xexf′(x).
(1)求k的值及F(x)的單調區間;
(2)已知函數g(x)=﹣x2+2ax(a為正實數),若對任意x2∈[0,1],總存在x1∈(0,+∞),使得g(x2)<F(x1),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且 ![]() asinA=(
asinA=( ![]() b﹣c)sinB+(
b﹣c)sinB+( ![]() c﹣b)sinC.
c﹣b)sinC.
(1)求角A的大小;
(2)若a= ![]() ,cosB=
,cosB= ![]() ,D為AC的中點,求BD的長.
,D為AC的中點,求BD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com