已知關于x的不等式k4x-2x+1+6k<0,
(1)若不等式的解集為(1,log23),求實數k的值;
(2)若不等式對一切x∈(1,log23)都成立,求實數k的取值范圍;
(3)若不等式的解集為(1,log23)的子集,求實數k的取值范圍.
解:(1)關于x的不等式k4
x-2
x+1+6k<0可以化為k(2
x)
2-2×2
x+6k<0,
令2
x=t,∵1<x<log
23,∴2<t<3,則不等式可化為kt
2-2t+6k<0,
∵關于x的不等式k4
x-2
x+1+6k<0的解集為(1,log
23),
∴(2,3)是不等式kt
2-2t+6k<0的解集,
∴2,3是方程kt
2-2t+6k=0的兩個實數根,且k<0.
解得
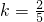
;
(2)∵不等式對一切x∈(1,log
23)都成立,
由(1)可知:即對于2<t<3,不等式kt
2-2t+6k<0恒成立,
等價于:
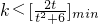
,t∈(2,3).
令
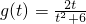
,t∈(2,3).
則
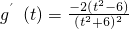
,令g
′(t)=0,解得
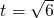
,
當
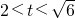
時,g
′(t)>0,函數g(t)在
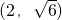
上單調遞增;
當
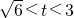
時,g
′(t)<0,函數g(t)在

上單調遞減;
而函數g(t)在t=2,3處有意義,且g(2)=

,g(3)=

.
故
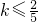
;
(3)因為不等式的解集為(1,log
23)的子集,
由(1)可知:即對于2<t<3,不等式kt
2-2t+6k<0的解集A⊆(2,3),
令f(t)=kt
2-2t+6k,△=4-24k
2,
則
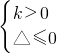
,或
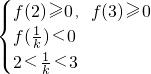
解得
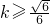
或
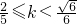
,
即
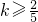
.
分析:(1)通過換元,利用一元二次不等式的解集與相應的一元二次方程的實數根的關系即可求出;
(2)把此問題可以轉化為恒成立問題解決即可;
(3)把問題轉化為利用二次函數的圖象與性質研究一元二次不等式的解集即可解決.
點評:熟練掌握一元二次不等式的解法及“三個二次”之間的關系是解題的關鍵.

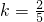 ;
;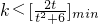 ,t∈(2,3).
,t∈(2,3).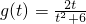 ,t∈(2,3).
,t∈(2,3).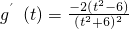 ,令g′(t)=0,解得
,令g′(t)=0,解得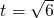 ,
,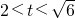 時,g′(t)>0,函數g(t)在
時,g′(t)>0,函數g(t)在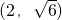 上單調遞增;
上單調遞增;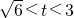 時,g′(t)<0,函數g(t)在
時,g′(t)<0,函數g(t)在 上單調遞減;
上單調遞減; ,g(3)=
,g(3)= .
.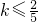 ;
;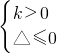 ,或
,或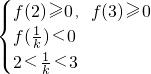
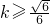 或
或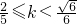 ,
,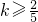 .
.
