
【題目】為研究男、女生的身高差異,現隨機從高二某班選出男生、女生各10人,并測量他們的身高,測量結果如下(單位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根據測量結果完成身高的莖葉圖(單位:厘米),并分別求出男、女生身高的平均值.
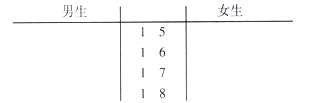
(2)請根據測量結果得到20名學生身高的中位數![]() (單位:厘米),將男、女生身高不低于
(單位:厘米),將男、女生身高不低于![]() 和低于
和低于![]() 的人數填入下表中,并判斷是否有
的人數填入下表中,并判斷是否有![]() 的把握認為男、女生身高有差異?
的把握認為男、女生身高有差異?
人數 | 男生 | 女生 |
身高 | ||
身高 |
參照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米為偏矮,不低于165厘米且低于175厘米為正常,不低于175厘米為偏高.假設可以用測量結果的頻率代替概率,試求從高二的男生中任意選出2人,恰有1人身高屬于正常的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在一個圓錐內作一個內接等邊圓柱(一個底面在圓錐的底面上,且軸截面是正方形的圓柱),再在等邊圓柱的上底面截得的小圓錐內做一個內接等邊圓柱,這樣無限的做下去.
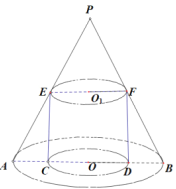
(1)證明這些等邊圓柱的體積從大到小排成一個等比數列;
(2)已知這些等邊圓柱的體積之和為原來圓錐體積的![]() ,求最大的等邊圓柱的體積與圓錐的體積之比.
,求最大的等邊圓柱的體積與圓錐的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線y2=2px(p>0)的焦點F的直線與拋物線交于A,B兩點,且![]() 3
3![]() ,拋物線的準線l與x軸交與點C,AA1垂直l于點A1,若四邊形AA1CF的面積為
,拋物線的準線l與x軸交與點C,AA1垂直l于點A1,若四邊形AA1CF的面積為![]() ,則準線l的方程為( )
,則準線l的方程為( )
A.![]() B.
B.![]() C.x=﹣2D.x=﹣1
C.x=﹣2D.x=﹣1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() ,且與坐標軸形成的三角形面積為
,且與坐標軸形成的三角形面積為![]() .求:
.求:
(1)求證:不論![]() 為何實數,直線
為何實數,直線![]() 過定點P;
過定點P;
(2)分別求![]() 和
和![]() 時,所對應的直線條數;
時,所對應的直線條數;
(3)針對![]() 的不同取值,討論集合
的不同取值,討論集合![]() 直線
直線![]() 經過P,且與坐標軸圍成的三角形面積為
經過P,且與坐標軸圍成的三角形面積為![]() 中的元素個數.
中的元素個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() 。
。
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() 左,右頂點分別為
左,右頂點分別為![]() ,
,![]() ,點
,點![]() ,
,![]() ,為橢圓
,為橢圓![]() 上位于
上位于![]() 軸上方的兩點,且
軸上方的兩點,且![]() ,記直線
,記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,若
,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究男、女生的身高差異,現隨機從高二某班選出男生、女生各10人,并測量他們的身高,測量結果如下(單位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根據測量結果完成身高的莖葉圖(單位:厘米),并分別求出男、女生身高的平均值.

(2)請根據測量結果得到20名學生身高的中位數![]() (單位:厘米),將男、女生身高不低于
(單位:厘米),將男、女生身高不低于![]() 和低于
和低于![]() 的人數填入下表中,并判斷是否有
的人數填入下表中,并判斷是否有![]() 的把握認為男、女生身高有差異?
的把握認為男、女生身高有差異?
人數 | 男生 | 女生 |
身高 | ||
身高 |
參照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米為偏矮,不低于165厘米且低于175厘米為正常,不低于175厘米為偏高.假設可以用測量結果的頻率代替概率,試求從高二的男生中任意選出2人,恰有1人身高屬于正常的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司推出一新款手機,因其功能強大,外觀新潮,一上市便受到消費者爭相搶購,銷量呈上升趨勢.散點圖是該款手機上市后前6周的銷售數據.
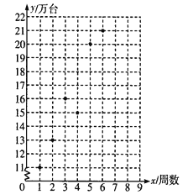
(1)根據散點圖,用最小二乘法求![]() 關于
關于![]() 的線性回歸方程,并預測該款手機第8周的銷量;
的線性回歸方程,并預測該款手機第8周的銷量;
(2)為了分析市場趨勢,該公司市場部從前6周的銷售數據中隨機抽取2周的數據,記抽取的銷量在18萬臺以上的周數為![]() ,求
,求![]() 的分布列和數學期望.參考公式:回歸直線方程
的分布列和數學期望.參考公式:回歸直線方程![]() ,其中:
,其中: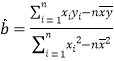 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】右邊程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”. 執行該程序框圖,若輸入的![]() 分別為16,20,則輸出的
分別為16,20,則輸出的![]() ( )
( )

A. 0B. 2C. 4D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.
(I)應從甲、乙、丙三個部門的員工中分別抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.
(i)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;
(ii)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com