
 表示為若干個正整數(shù)(至少3個,且可以相等)之和的形式,若這幾個正整數(shù)可以按一定順序構成等差數(shù)列,則稱這些數(shù)為
表示為若干個正整數(shù)(至少3個,且可以相等)之和的形式,若這幾個正整數(shù)可以按一定順序構成等差數(shù)列,則稱這些數(shù)為 的一個等差分拆.將這些正整數(shù)的不同排列視為相同的分拆.如:(1,4,7)與(7,4,1)為12的相同等差分拆.問正整數(shù)30的不同等差分拆有 ▲ 個.
的一個等差分拆.將這些正整數(shù)的不同排列視為相同的分拆.如:(1,4,7)與(7,4,1)為12的相同等差分拆.問正整數(shù)30的不同等差分拆有 ▲ 個. ,數(shù)列的公差為
,數(shù)列的公差為 。若是由3個正整數(shù)構成的等差分拆,則有
。若是由3個正整數(shù)構成的等差分拆,則有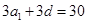 ,即
,即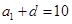 ,所以
,所以 或
或 或…或
或…或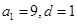 或
或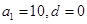 ,共有10組等差分拆;
,共有10組等差分拆;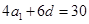 ,即
,即 ,所以
,所以 或
或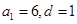 ,共有2組等差分拆;
,共有2組等差分拆;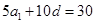 ,即
,即 ,所以
,所以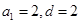 或
或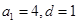 或
或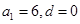 ,共有3組等差分拆;
,共有3組等差分拆; ,即
,即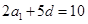 ,所以
,所以 ,共有1組等差分拆;
,共有1組等差分拆; ,此時有0組等差分拆;
,此時有0組等差分拆;

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:填空題
 ,有下列三個命題:①.該二項式展開式中非常數(shù)項的系數(shù)和是
,有下列三個命題:①.該二項式展開式中非常數(shù)項的系數(shù)和是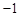 ;②.該二項式展開式中第
;②.該二項式展開式中第 項是
項是 ;③.當
;③.當 時,
時, 除以
除以 的余數(shù)是
的余數(shù)是 .其中正確命題的序號是 (把你認為正確的序號都填上).
.其中正確命題的序號是 (把你認為正確的序號都填上).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.6 | B.8 | C.12 | D.16 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.21600 | B.10800 | C.7200 | D.5400 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com