
2013年4月20日8時02分四川省雅安市蘆山縣(北緯30.3,東經103.0)發生7.0級地震。一方有難,八方支援,重慶眾多醫務工作者和志愿者加入了抗災救援行動。其中重慶某醫院外科派出由5名骨干醫生組成的救援小組,奔赴受災第一線參與救援。現將這5名醫生分別隨機分配到受災最嚴重的蘆山、寶山、天全三縣中的某一個。
(1)求每個縣至少分配到一名醫生的概率。
(2)若將隨機分配到蘆山縣的人數記為 ,求隨機變量
,求隨機變量 的分布列,期望和方差。
的分布列,期望和方差。
 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
為了響應學校“學科文化節”活動,數學組舉辦了一場數學知識比賽,共分為甲、乙兩組.其中甲組得滿分的有1個女生和3個男生,乙組得滿分的有2個女生和4個男生.現從得滿分的學生中,每組各任選2個學生,作為數學組的活動代言人.
(1)求選出的4個學生中恰有1個女生的概率;(2)設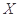 為選出的4個學生中女生的人數,求
為選出的4個學生中女生的人數,求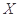 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知A,B,C,D,E,F是邊長為1的正六邊形的6個頂點,在頂點取自A,B,C,D,E,F的所有三角形中,隨機(等可能)取一個三角形.設隨機變量X為取出三角形的面積.
(Ⅰ) 求概率P ( X=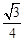 );
);
(Ⅱ) 求數學期望E ( X ).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
市民李生居住在甲地,工作在乙地,他的小孩就讀的小學在丙地,三地之間的道路情況如圖所示.假設工作日不走其它道路,只在圖示的道路中往返,每次在路口選擇道路是隨機的.同一條道路去程與回程是否堵車互不影響.假設李生早上需要先開車送小孩去丙地小學,再返回經甲地趕去乙地上班,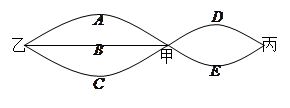
(1)寫出李生可能走的所有路線;(比如DDA表示走D路從甲到丙,再走D路回到甲,然后走A路到達乙);
(2)假設從丙地到甲地時若選擇走道路D會遇到擁堵,并且從甲地到乙地時若選擇走道路B也會遇到擁堵,其它方向均通暢,但李生不知道相關信息,那么從出發到回到上班地沒有遇到過擁堵的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人參加某種選拔測試.在備選的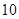 道題中,甲答對其中每道題的概率都是
道題中,甲答對其中每道題的概率都是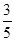 ,乙能答對其中的
,乙能答對其中的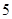 道題.規定每次考試都從備選的
道題.規定每次考試都從備選的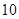 道題中隨機抽出
道題中隨機抽出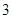 道題進行測試,答對一題加
道題進行測試,答對一題加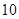 分,答錯一題(不答視為答錯)減
分,答錯一題(不答視為答錯)減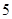 分,至少得
分,至少得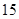 分才能入選.
分才能入選.
(1)求甲得分的數學期望;
(2)求甲、乙兩人同時入選的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三人獨立破譯同一份密碼,已知甲、乙、丙各自破譯出密碼的概率分別為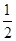 、
、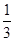 、
、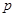 ,且他們是否破譯出密碼互不影響,若三人中只有甲破譯出密碼的概率為
,且他們是否破譯出密碼互不影響,若三人中只有甲破譯出密碼的概率為 .
.
(1)求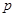 的值.
的值.
(2)設甲、乙、丙三人中破譯出密碼的人數為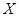 ,求
,求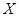 的分布列和數學期望
的分布列和數學期望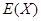 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校從高二年級學生中隨機抽取60名學生,將其會考的政治成績(均為整數)分成六段: 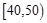 ,
,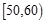 ,…,
,…,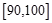 后得到如下頻率分布直方圖.
后得到如下頻率分布直方圖.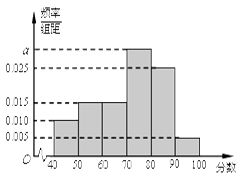
(Ⅰ)求圖中 的值
的值
(Ⅱ)根據頻率分布直方圖,估計該校高二年級學生政治成績的平均分;
(Ⅲ)用分層抽樣的方法在80分以上(含 80分)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任意選取2人,求其中恰有1人的分數不低于90分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
市民李生居住在甲地,工作在乙地,他的小孩就讀的小學在丙地,三地之間的道路情
況如圖所示.假設工作日不走其它道路,只在圖示的道路中往返,每次在路口選擇道路是隨機
的.同一條道路去程與回程是否堵車相互獨立. 假設李生早上需要先開車送小孩去丙地小學,
再返回經甲地趕去乙地上班.假設道路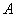 、
、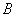 、
、 上下班時間往返出現擁堵的概率都是
上下班時間往返出現擁堵的概率都是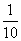 ,
,
道路 、
、 上下班時間往返出現擁堵的概率都是
上下班時間往返出現擁堵的概率都是 ,只要遇到擁堵上學和上班的都會遲到.
,只要遇到擁堵上學和上班的都會遲到.
(1)求李生小孩按時到校的概率;
(2)李生是否有八成把握能夠按時上班?
(3)設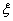 表示李生下班時從單位乙到達小學丙遇到擁堵的次數,求
表示李生下班時從單位乙到達小學丙遇到擁堵的次數,求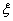 的均值.
的均值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某網站用“10分制”調查一社區人們的幸福度.現從調查人群中隨機抽取16名, 以下莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖, 小數點后的一位數字為葉):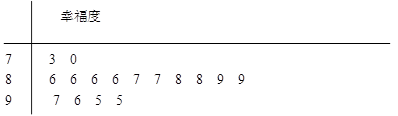
(1) 指出這組數據的眾數和中位數;
(2) 若幸福度不低于9.5分, 則稱該人的幸福度為“極幸福”.求從這16人中隨機選取3人, 至多有1人是“極幸福”的概率;
(3) 以這16人的樣本數據來估計整個社區的總體數據, 若從該社區(人數很多)任選3人, 記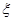 表示抽到“極幸福”的人數, 求
表示抽到“極幸福”的人數, 求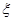 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com