
(本小題14分)某人有樓房一幢,室內面積共計180m2,擬分割成兩類房間作為旅游客房,大房間每間面積為18m2,可住游客5名,每名游客每天住宿費40元;小房間每間面積為15m2,可以住游客3名,每名游客每天住宿費50元;裝修大房間每間需要1000元,裝修小房間每間需要600元.如果他只能籌款8000元用于裝修,且游客能住滿客房,他應隔出大房間和小房間各多少間,每天能獲得最大的房租收益?(注:設分割大房間為x間,小房間為y間,每天的房租收益為z元)
(1)寫出x,y所滿足的線性約束條件;
(2)寫出目標函數的表達式;
(3)求x,y各為多少時,每天能獲得最大的房租收益?每天能獲得最大的房租收益是多少?
(1) 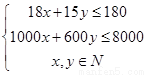
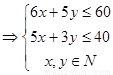
(2)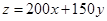
(3)當大房間為3間,小房間為8間或大房間為0間,小房間為12間時,可獲最大的收益為1800元.
【解析】
試題分析:先設分割大房間為x間,小房間為y間,收益為z元,列出約束條件,再根據約束條件畫出可行域,設z=200x+150y,再利用z的幾何意義求最值,只需求出直線z=200x+150y過可行域內的整數點時,從而得到z值即可.
設分割大房間為x間,小房間為y間,收益為z元
根據題意得:
(1) 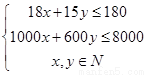
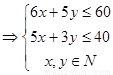 .........3分
.........3分
(2)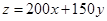 ............6分
............6分
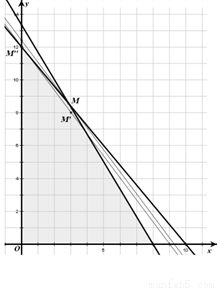
(3)作出約束條件表示的平面區域 ............9分
把目標函數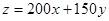 化為
化為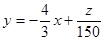
平移直線,直線越往上移,z越大,
所以當直線經過M點時,z的值最大,
解方程組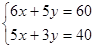 得
得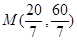 ,
,
因為最優解應該是整數解,通過調整得,當直線過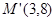 和
和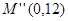 時z最大.........13分
時z最大.........13分
所以當大房間為3間,小房間為8間或大房間為0間,小房間為12間時,可獲最大的收益為1800元. ............14分
考點:簡單線性規劃的應用.
點評:在解決線性規劃的應用題時,其步驟為:①分析題目中相關量的關系,列出不等式組,即約束條件⇒②由約束條件畫出可行域⇒③分析目標函數Z與直線截距之間的關系⇒④使用平移直線法求出最優解⇒⑤還原到現實問題中.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2012-2013學年黑龍江省齊齊哈爾市高三二模理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)
一個不透明的袋子中裝有4個形狀相同的小球,分別標有不同的數字2,3,4, ,現從袋中隨機摸出2個球,并計算摸出的這2個球上的數字之和,記錄后將小球放回袋中攪勻,進行重復試驗。記A事件為“數字之和為7”.試驗數據如下表
,現從袋中隨機摸出2個球,并計算摸出的這2個球上的數字之和,記錄后將小球放回袋中攪勻,進行重復試驗。記A事件為“數字之和為7”.試驗數據如下表
|
摸球總次數 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
|
“和為7”出現的頻數 |
1 |
9 |
14 |
24 |
26 |
37 |
58 |
82 |
109 |
150 |
|
“和為7”出現的頻率 |
0.10 |
0.45 |
0.47 |
0.40 |
0.29 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
(參考數據: )
)
(Ⅰ)如果試驗繼續下去,根據上表數據,出現“數字之和為7”的頻率將穩定在它的概率附近。試估計“出現數字之和為7”的概率,并求 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,設定一種游戲規則:每次摸2球,若數字和為7,則可獲得獎金7元,否則需交5元。某人摸球3次,設其獲利金額為隨機變量 元,求
元,求 的數學期望和方差。
的數學期望和方差。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分) 如圖,在墻上掛著一塊邊長為16cm的正方形木板,上面畫了小、中、大三個同心圓,半徑分別為2cm,4cm,6cm,某人站在3m之外向此板投鏢,設投鏢擊中線上或沒有投中木板時都不算(可重投),
 問:(1)投中大圓內的概率是多少?
問:(1)投中大圓內的概率是多少?
(2)投中小圓與中圓形成的圓環的概率是多少?
(3)投中大圓之外的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com