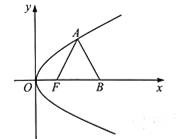
【題目】在平面直角坐標(biāo)系
中，已知點F為拋物線
的焦點，點A在拋物線E上，
點B在x軸上，且
是邊長為2的等邊三角形。
（1）求拋物線E的方程；
（2）設(shè)C是拋物線E上的動點，直線
為拋物線E在點C處的切線，求點B到直線距離的最小值，并求此時點C的坐標(biāo)。
寒假樂園北京教育出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系中，已知直線l過點
.
（1）若直線l的縱截距和橫截距相等，求直線l的方程；
（2）若直線l與兩坐標(biāo)軸圍成的三角形的面積為
，求直線l的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】甲、乙兩人練習(xí)罰球，每人練習(xí)6組，每組罰球20個，命中個數(shù)莖葉圖如下：
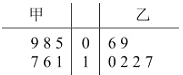
（1）求甲命中個數(shù)的中位數(shù)和乙命中個數(shù)的眾數(shù)；
（2）通過計算，比較甲乙兩人的罰球水平.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知定義在R上的函數(shù)
滿足:①對于任意的
都有
成立;②當(dāng)
時,
;③
;則不等式
的解集為__________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖為某大河的一段支流，岸線
近似滿足
∥
寬度為7
圓
為河中的一個半徑為2
的小島，小鎮(zhèn)
位于岸線上，且滿足岸線
現(xiàn)計劃建造一條自小鎮(zhèn)經(jīng)小島至對岸
的通道
（圖中粗線部分折線段，
在右側(cè)），為保護(hù)小島，
段設(shè)計成與圓相切，設(shè)
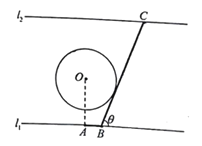
（1）試將通道的長
表示成
的函數(shù)，并指出其定義域.
（2）求通道的最短長.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
是定義在R上的偶函數(shù)，對任意
都有
，當(dāng)
，且
時，
，給出如下命題：
①
；
②直線
是函數(shù)的圖象的一條對稱軸；
③函數(shù)在
上為增函數(shù)；
④函數(shù)在
上有四個零點.
其中所有正確命題的序號為（ ）
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】正四棱錐
的底面正方形邊長是3，
是在底面上的射影，
，
是
上的一點，過且與
、
都平行的截面為五邊形
．
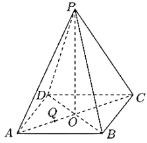
（1）在圖中作出截面，并寫出作圖過程；
（2）求該截面面積的最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
，函數(shù)
.
（1）若
，
極大值；
（2）若
無零點，求實數(shù)
的取值范圍；
（3）若有兩個相異零點
，
，求證：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系中，圓
的參數(shù)方程為
（
為參數(shù)）.以坐標(biāo)原點為極點，
軸的正半軸為極軸建立極坐標(biāo)系，直線
的極坐標(biāo)方程為
.
（1）求圓的普通方程和直線的直角坐標(biāo)方程；
（2）若直線與圓交于
兩點，
是圓上不同于兩點的動點，求
面積的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
