
【題目】若無窮數列![]() 滿足:
滿足:![]() ,當
,當![]() ,
,![]() 時.
時.
![]() 其中
其中![]() 表示
表示![]() ,
,![]() ,
,![]() ,
,![]() 中的最大項
中的最大項![]() ,有以下結論:
,有以下結論:
![]() 若數列
若數列![]() 是常數列,則
是常數列,則![]()
![]() 若數列
若數列![]() 是公差
是公差![]() 的等差數列,則
的等差數列,則![]() ;
;
![]() 若數列
若數列![]() 是公比為q的等比數列,則
是公比為q的等比數列,則![]()
則其中正確的結論是______![]() 寫出所有正確結論的序號
寫出所有正確結論的序號![]()
 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:
【題目】高鐵、網購、移動支付和共享單車被譽為中國的“新四大發明”,彰顯出中國式創新的強勁活力.某移動支付公司從某市移動支付用戶中隨機抽取100人進行調查,得到如下數據:
每周移動支付次數 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
總計 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移動支付6次及以上的用戶稱為“移動支付達人”,按分層抽樣的方法,從參與調查的“移動支付達人”中,隨機抽取6人,求抽取的6人中,男、女用戶各多少人;
(2)把每周使用移動支付超過3次的用戶稱為“移動支付活躍用戶”,根據表格中的數據完成下列![]() 列聯表,問:能否有
列聯表,問:能否有![]() 的把握認為“移動支付活躍用戶”與性別有關?
的把握認為“移動支付活躍用戶”與性別有關?
非移動支付活躍用戶 | 移動支付活躍用戶 | 總計 | |
男 | |||
女 | |||
總計 |
附參照表:
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
參考公式: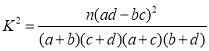 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級有400名學生參加某項體育測試,根據男女學生人數比例,使用分層抽樣的方法從中抽取了100名學生,記錄他們的分數,將數據分成7組:![]() ,整理得到如下頻率分布直方圖:
,整理得到如下頻率分布直方圖:
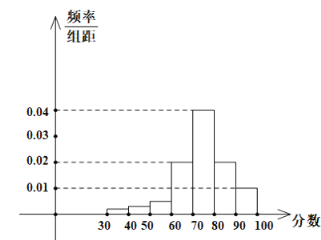
(1)若該樣本中男生有55人,試估計該學校高三年級女生總人數;
(2)若規定小于60分為“不及格”,從該學校高三年級學生中隨機抽取一人,估計該學生不及格的概率;
(3)若規定分數在![]() 為“良好”,
為“良好”,![]() 為“優秀”.用頻率估計概率,從該校高三年級隨機抽取三人,記該項測試分數為“良好”或“優秀”的人數為X,求X的分布列和數學期望.
為“優秀”.用頻率估計概率,從該校高三年級隨機抽取三人,記該項測試分數為“良好”或“優秀”的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次會操活動中,領操員讓編號為![]() 的
的![]() 名學生排成一個圓形陣,做
名學生排成一個圓形陣,做![]() 循環報數,領操員一一記錄報數者的編號,并要求報l、2的學生出列,報3的學生留在隊列中,并將編號改為此次循環報數中三名學生的編號之和.一直循環報數下去.當操場上剩余的學生人數不超過兩名時,報數活動結束.領操員記錄最后留在操場的學生編號(例如,編號為
循環報數,領操員一一記錄報數者的編號,并要求報l、2的學生出列,報3的學生留在隊列中,并將編號改為此次循環報數中三名學生的編號之和.一直循環報數下去.當操場上剩余的學生人數不超過兩名時,報數活動結束.領操員記錄最后留在操場的學生編號(例如,編號為![]() 的九名學生排成一個圓形陣,報數結束后,只有原始編號為9的學生留在操場,此時,他的編號為45,領操員記錄下來的數據分別為l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名學生參加會操.
的九名學生排成一個圓形陣,報數結束后,只有原始編號為9的學生留在操場,此時,他的編號為45,領操員記錄下來的數據分別為l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名學生參加會操.
(1)最后留在場內的學生最初的編號是幾號?
(2)求領操員記錄下的編號之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在股票市場上,投資者常根據股價![]() 每股的價格
每股的價格![]() 走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價
走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價![]() 元
元![]() 與時間
與時間![]() 天
天![]() 的關系在ABC段可近似地用函數
的關系在ABC段可近似地用函數![]() 的圖象從最高點A到最低點C的一段來描述
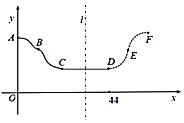
的圖象從最高點A到最低點C的一段來描述![]() 如圖
如圖![]() ,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:
,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:![]() 對稱,點B,D的坐標分別是
對稱,點B,D的坐標分別是![]() .
.
![]() 請你幫老張確定a,
請你幫老張確定a,![]() ,
,![]() 的值,并寫出ABC段的函數解析式;
的值,并寫出ABC段的函數解析式;
![]() 如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列敘述正確的是( )
A.相關關系是一種確定性關系,一般可分為正相關和負相關
B.回歸直線一定過樣本點的中心![]()
C.在回歸分析中,![]() 為0.98的模型比
為0.98的模型比![]() 為0.80的模型擬合的效果好
為0.80的模型擬合的效果好
D.某同學研究賣出的熱飲杯數![]() 與氣溫
與氣溫![]() 的關系,得到回歸方程
的關系,得到回歸方程![]() ,則氣溫為2℃時,一定可賣出142杯熱飲
,則氣溫為2℃時,一定可賣出142杯熱飲
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年12月份,我國湖北武漢出現了新型冠狀病毒,人感染后會出現發熱、咳嗽、氣促和呼吸困難等,嚴重的可導致肺炎甚至危及生命.為了增強居民防護意識,增加居民防護知識,某居委會利用網絡舉辦社區線上預防新冠肺炎知識答題比賽,所有居民都參與了防護知識網上答卷,最終甲、乙兩人得分最高進入決賽,該社區設計了一個決賽方案:①甲、乙兩人各自從![]() 個問題中隨機抽
個問題中隨機抽![]() 個.已知這
個.已知這![]() 個問題中,甲能正確回答其中的
個問題中,甲能正確回答其中的![]() 個,而乙能正確回答每個問題的概率均為
個,而乙能正確回答每個問題的概率均為![]() ,甲、乙兩人對每個問題的回答相互獨立、互不影響;②答對題目個數多的人獲勝,若兩人答對題目數相同,則由乙再從剩下的
,甲、乙兩人對每個問題的回答相互獨立、互不影響;②答對題目個數多的人獲勝,若兩人答對題目數相同,則由乙再從剩下的![]() 道題中選一道作答,答對則判乙勝,答錯則判甲勝.
道題中選一道作答,答對則判乙勝,答錯則判甲勝.
(1)求甲、乙兩人共答對![]() 個問題的概率;
個問題的概率;
(2)試判斷甲、乙誰更有可能獲勝?并說明理由;
(3)求乙答對題目數的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,且經過點
,且經過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,試問在
,試問在![]() 軸上是否存在定點
軸上是否存在定點![]() 使得直線
使得直線![]() 與直線
與直線![]() 恰關于
恰關于![]() 軸對稱?若存在,求出點
軸對稱?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com