解:(1)∵點(n,S
n)在函數f(x)=x
2+x的圖象上,
∴S
n=n
2+n.
a
1=S
1=2,當n≥2時,a
n=S
n-S
n-1=2n(n=1時也成立).
∴a
n=2n(n∈N
*).
(2)
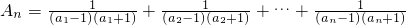
=
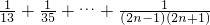
=
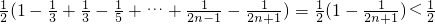
.
依題意,只要
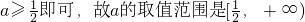
.
(3)數列{a
n}依次按1項,2項循環地分為(2),(4,6),(8),(10,12);(14),(16,18);(20),…,每一次循環記為一組.由于每一個循環含有2個括號,故b
100是第50組中第2個括號內各數之和.
由分組規律知,b
2,b
4,b
6,…,b
100,…組成一個首項b
2=4+6=10,公差d=12
的等差數列.
所以b
100=10+(50-1)×12=598.
(4)當n是4的整數倍時,求b
n的值.
數列{a
n}依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12);(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…
第4組,第8組,…,第4k(k∈N
*)組的第1個數,第2個 數,…,第4個數分別組成一個等差數列,
其首項分別為14,16,18,20.公差均為20.
則第4組,第8組,…,第4k組的各數之和也組成一個等差數列,
其公差為80.
且b
4=14+16+18+20=68.
當n=4k時,b
n=68+80(k-1)=20n-12.
分析:(1)由點(n,S
n)在函數f(x)=x
2+x的圖象上可得S
n=n
2+2n利用遞推公式

可求;
(2)根據(1)求出
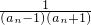
,利用裂項相消法求出A
n即可求出使得不等式A
n<a對一切n∈N
*都成立的a;
(3)由分組規律知,b
2,b
4,b
6,…b
100組成首項為b
2=4+6=10,公差d=12的等差數列,利用等差數列的通項公式可求;
(4)根據題意,舉特例當n是4的整數倍時,求b
n的值.根據依次按1項,2項,3項,4項循環,可知數列{a
n}依次按1項、2項、3項、4項循環地分為(2),(4,6),(8,10,12);(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…,根據它們的特點即可求得結果.
點評:本題主要考查了利用遞推公式

求數列的通項公式,注意不要漏掉對n=1的檢驗
,以及裂項相消求和法,還考查了等差數列的通項公式的應用,同時考查運算能力,屬中檔題.

 ,使得不等式An<a對一切n∈N*都成立?若存在,求出a的取值范圍;若不存在,請說明理由;
,使得不等式An<a對一切n∈N*都成立?若存在,求出a的取值范圍;若不存在,請說明理由;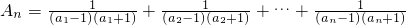
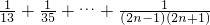 =
=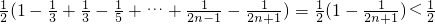 .
.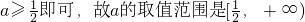 .
. 可求;
可求;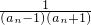 ,利用裂項相消法求出An即可求出使得不等式An<a對一切n∈N*都成立的a;
,利用裂項相消法求出An即可求出使得不等式An<a對一切n∈N*都成立的a; 求數列的通項公式,注意不要漏掉對n=1的檢驗
求數列的通項公式,注意不要漏掉對n=1的檢驗
