
 對于一切正整數n,均有Tn≤C恒成立,求C的最小值.
對于一切正整數n,均有Tn≤C恒成立,求C的最小值.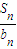 對于一切正整數n,均有Tn≤C恒成立,則需C大于或等于Tn的最大值,然后研究Tn的單調性可求出最大值,從而求出所求.
對于一切正整數n,均有Tn≤C恒成立,則需C大于或等于Tn的最大值,然后研究Tn的單調性可求出最大值,從而求出所求.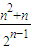 ,若Tn=
,若Tn=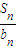 對于一切正整數n,均有Tn≤C恒成立,
對于一切正整數n,均有Tn≤C恒成立,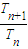 =
=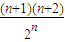 ×
×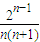 =
=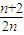 ,…(10分)
,…(10分)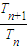 ≥1得:n≤2,
≥1得:n≤2, ≥T5=
≥T5=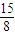 ≥…≥Tn≥…,…(12分)
≥…≥Tn≥…,…(12分)

 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、充分而不必要條件 | B、必要而不充分條件 | C、充分必要條件 | D、既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com