
【題目】在四棱錐P﹣ABCD中,△PAD為正三角形,平面PAD⊥平面ABCD,E為AD的中點,AB∥CD,AB⊥AD,CD=2AB=2AD=4.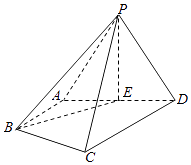
(Ⅰ)求證:平面PCD⊥平面PAD;
(Ⅱ)求直線PB與平面PCD所成角的正弦值;
(Ⅲ)在棱CD上是否存在點M,使得AM⊥平面PBE?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】證明:(Ⅰ)∵△PAD為正三角形,E為AD的中點,∴PE⊥AD.
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,∴PE⊥平面ABCD.
∵CD平面ABCD,∴PE⊥CD.
∵AB∥CD,AB⊥AD,∴CD⊥AD.
∵PE∩AD=E,∴CD⊥平面PAD.
∵CD平面ABCD,
∴平面PCD⊥平面PAD.…
解:(Ⅱ)在平面ABCD內作直線EF⊥AD.
∴EF⊥平面PAD,∴EF⊥PE.
以E為原點建立空間直角坐標系E﹣xyz,如圖所示.
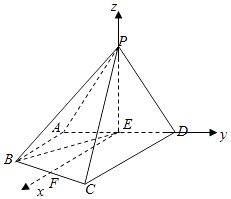
則P(0,0, ![]() ),A(0,﹣1,0),B(2,﹣1,0),C(4,1,0),D(0,1,0).
),A(0,﹣1,0),B(2,﹣1,0),C(4,1,0),D(0,1,0).
![]() =(2,﹣1,﹣
=(2,﹣1,﹣ ![]() ),
), ![]() =(4,1,﹣
=(4,1,﹣ ![]() ),
), ![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
),
設平面PCD的法向量為 ![]() =(x,y,z).
=(x,y,z).
∴ 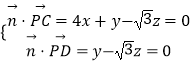 ,令z=
,令z= ![]() ,則
,則 ![]() =(0,3,
=(0,3, ![]() ),
),
設直線PB與平面PCD所成的角為α.
則sinα=|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() .
.
∴直線PB與平面PCD所成角的正弦值為 ![]() .…
.…
(Ⅲ)在棱CD上假設存在點M,使得AM⊥平面PBE.
∵PE⊥平面ABCD,∴PE⊥AM.
要使AM⊥平面PBE成立,只需AM⊥EB成立.
設M(x0,y0,z0), ![]() .λ∈[0,1]
.λ∈[0,1]
∴ ![]() ,即(x,y﹣1,z)=λ(4,0,0).∴x=4λ,y=1,z=0.∴M(4λ,1,0).
,即(x,y﹣1,z)=λ(4,0,0).∴x=4λ,y=1,z=0.∴M(4λ,1,0).
∵ ![]() ,
,
∴由 ![]() ⊥
⊥ ![]() ,得
,得 ![]() =0,即8λ﹣2=0.解得
=0,即8λ﹣2=0.解得 ![]() ∈[0,1].
∈[0,1].
故 ![]() .…
.…
【解析】1、由面面垂直得到線面垂直,再由線線垂直得到平面PCD⊥平面PAD.
2、線面角指的是這條直線在這個平面內的射影和該線所成的角。原點建立空間直角坐標系E﹣xyz,由題意可得
設直線PB與平面PCD所成的角為α.則sinα=|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() .直線PB與平面PCD所成角的正弦值為
.直線PB與平面PCD所成角的正弦值為 ![]() .
.
3、在棱CD上假設存在點M,使得AM⊥平面PBE.∵PE⊥平面ABCD,∴PE⊥AM.要使AM⊥平面PBE成立,只需AM⊥EB成立.由向量知識可得由 ![]() ,
,![]() ,
,![]() 得
得![]() 即8λ﹣2=0.解得 λ = 1 4 ∈[0,1].故
即8λ﹣2=0.解得 λ = 1 4 ∈[0,1].故 ![]() .…
.…


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:高中數學 來源: 題型:
【題目】中國有個名句“運籌帷幄之中,決勝千里之外”.其中的“籌”原意是指《孫子算經》中記載的算籌,古代是用算籌來進行計算,算籌是將幾寸長的小竹棍擺在平面上進行運算,算籌的擺放形式有縱橫兩種形式,如下表: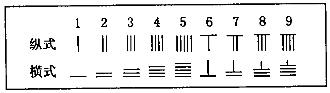
表示一個多位數時,像阿拉伯計數一樣,把各個數位的數碼從左到右排列,但各位數碼的籌式需要縱橫相間,個位,百位,萬位數用縱式表示,十位,千位,十萬位用橫式表示,以此類推,例如6613用算籌表示就是: ![]() ,則5288用算籌式可表示為( )
,則5288用算籌式可表示為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD, ![]() ,四邊形ACFE為矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四邊形ACFE為矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.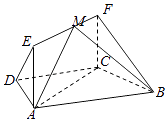
(1)求證:EF⊥平面BCF;
(2)點M在線段EF(含端點)上運動,當點M在什么位置時,平面MAB與平面FCB所成銳二面角最大,并求此時二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四支足球隊進行單循環比賽(每兩隊比賽一場),每場比賽勝者得3分,負者得0分,平局雙方各得1分.比賽結束后發現沒有足球隊全勝,且四隊得分各不相同,則所有比賽中最多可能出現的平局場數是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )的圖象過點
)的圖象過點 ![]() ,且在(
,且在( ![]() ,
, ![]() )上單調,同時f(x)的圖象向左平移π個單位之后與原來的圖象重合,當
)上單調,同時f(x)的圖象向左平移π個單位之后與原來的圖象重合,當 ![]() ,且x1≠x2時,f(x1)=f(x2),則f(x1+x2)=( )
,且x1≠x2時,f(x1)=f(x2),則f(x1+x2)=( )
A.﹣ ![]()
B.﹣1
C.1
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1的焦點在x軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
=1的焦點在x軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
(Ⅰ)當t=4,|AM|=|AN|時,求△AMN的面積;
(Ⅱ)當2|AM|=|AN|時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() lnx-x+
lnx-x+ ![]() ,其中a>0.
,其中a>0.
(1)若f(x)在(0,+∞)上存在極值點,求a的取值范圍;
(2)設a∈(1,e],當x1∈(0,1),x2∈(1,+∞)時,記f(x2)-f(x1)的最大值為M(a).那么M(a)是否存在最大值?若存在,求出其最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com