
【題目】如圖,![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,離心率為
,離心率為![]() ,雙曲線
,雙曲線![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,已知
,已知![]() ,
,![]() .
.
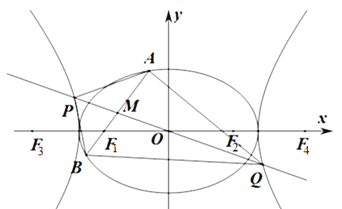
(1)求![]() ,
,![]() 的方程;
的方程;
(2)過![]() 作
作![]() 的不垂直于
的不垂直于![]() 軸的弦
軸的弦![]() ,
,![]() 為弦
為弦![]() 的中點,當直線
的中點,當直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點時,求四邊形
兩點時,求四邊形![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可推出
可推出![]() ,從而
,從而![]() ,
,![]() ,因此
,因此![]() ,推出
,推出![]() ,
,![]() ,從而得到
,從而得到![]() 的方程;
的方程;
(2)設直線![]() 的方程為
的方程為![]() ,聯立
,聯立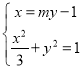 ,利用韋達定理和中點坐標公式求出
,利用韋達定理和中點坐標公式求出![]() ,從而得到直線
,從而得到直線![]() 的方程為
的方程為![]() ,再聯立
,再聯立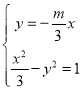 ,由韋達定理和弦長公式求出
,由韋達定理和弦長公式求出![]() ,再利用點到直線的距離公式求出
,再利用點到直線的距離公式求出![]() 到直線
到直線![]() 的距離以及
的距離以及![]() 到直線
到直線![]() 的距離,進而得到四邊形
的距離,進而得到四邊形![]() 的面積的最小值.
的面積的最小值.
(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的方程為
的方程為![]() ,
,![]() 的方程為
的方程為![]() .
.
(2)依題意,直線![]() 的方程可設為
的方程可設為![]() ,設
,設![]() ,
,![]() ,
,
由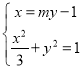 消去
消去![]() 可得
可得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 中點坐標為
中點坐標為![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,
,
由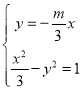 消去
消去![]() ,可得
,可得![]() ,
,
∴![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,
設![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]() 到直線
到直線![]() 的距離也為
的距離也為![]() ,
,
∴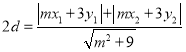 ,
,
∵![]() ,
,
∴ ,
,
又∵ ,
,
∴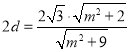 ,
,
∴四邊形![]() 的面積
的面積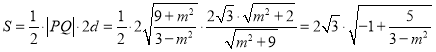 ,
,
∴當![]() 時,
時,![]() 取得最小值,且
取得最小值,且![]() ,即四邊形
,即四邊形![]() 面積的最小值為
面積的最小值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
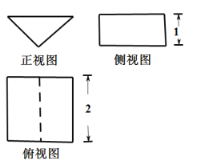
【題目】一個幾何體的三視圖如圖所示,正視圖為等腰直角三角形,俯視圖中虛線平分矩形的面積,則該幾何體的體積為_____,其外接球的表面積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
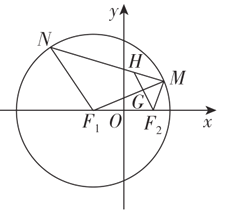
【題目】如圖,已知點![]() ,點
,點![]() 均在圓
均在圓![]() 上,且
上,且![]() ,過點
,過點![]() 作
作![]() 的平行線分別交
的平行線分別交![]() ,
,![]() 于
于![]() 兩點.
兩點.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)過點![]() 的動直線
的動直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點.問是否存在常數
兩點.問是否存在常數![]() ,使得
,使得![]() 點為定值?若存在,求出
點為定值?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重. 大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫院隨機的對入院50人進行了問卷調查得到了如表所示的列聯表:已知在全部50人中隨機抽取1人,抽到患心肺疾病的人的概率為![]() .
.
(1)請將列聯表補充完整;
患心肺 疾病 | 不患心 肺疾病 | 合計 | |
男 | 5 | ||
女 | 10 | ||
合計 | 50 |
(2)是否有97.5%的把握認為患心肺疾病與性別有關?說明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患胃病.現在從患心肺疾病的10位女性中,選出3名進行其他方面的排查,記選出患胃病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.下面的臨界值表供參考:
的分布列以及數學期望.下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 過點A
過點A![]() ,兩個焦點為(-1,0),(1,0)。
,兩個焦點為(-1,0),(1,0)。
(Ⅰ)求橢圓C的方程;
(Ⅱ)E,F是橢圓C上的兩個動點,如果直線AE的斜率與AF的斜率互為相反數,證明直線EF的斜率為定值,并求出這個定值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大學先修課程,是在高中開設的具有大學水平的課程,旨在讓學有余力的高中生早接受大學思維方式、學習方法的訓練,為大學學習乃至未來的職業生涯做好準備.某高中成功開設大學先修課程已有兩年,共有250人參與學習先修課程.
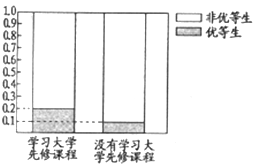
(Ⅰ)這兩年學校共培養出優等生150人,根據下圖等高條形圖,填寫相應列聯表,并根據列聯表檢驗能否在犯錯的概率不超過0.01的前提下認為學習先修課程與優等生有關系?
優等生 | 非優等生 | 總計 | |
學習大學先修課程 | 250 | ||
沒有學習大學先修課程 | |||
總計 | 150 |
(Ⅱ)某班有5名優等生,其中有2名參加了大學生先修課程的學習,在這5名優等生中任選3人進行測試,求這3人中至少有1名參加了大學先修課程學習的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式:![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com