下列四個(gè)命題：
①在空間中，存在無數(shù)個(gè)點(diǎn)到三角形各邊的距離相等；
②在空間中，存在無數(shù)個(gè)點(diǎn)到長(zhǎng)方形各邊的距離相等；
③在空間中，既存在到長(zhǎng)方體各頂點(diǎn)距離相等的點(diǎn)，又存在到它的各個(gè)面距離相等的點(diǎn)；
④在空間中，既存在到四面體各頂點(diǎn)距離相等的點(diǎn)，又存在到它的各個(gè)面距離相等的點(diǎn)．
其中真命題的序號(hào)是________．（寫出所有真命題的序號(hào)）
①④
分析：對(duì)于①，過三角形的內(nèi)心且垂直于該三角形所在平面的直線上任意一點(diǎn)到該三角形的各邊的距離都相等；對(duì)于②，假設(shè)存在點(diǎn)到長(zhǎng)方形的各邊的距離相等，則該點(diǎn)到四個(gè)頂點(diǎn)的距離相等，該點(diǎn)必在過這個(gè)長(zhǎng)方形的中心且與這個(gè)長(zhǎng)方形所在的平面垂直的直線上，由此可知該長(zhǎng)方形的長(zhǎng)、寬相等，而對(duì)于任意的長(zhǎng)方形而言其長(zhǎng)、寬未必相等；對(duì)于③，若存在到長(zhǎng)方體的各個(gè)面距離相等的點(diǎn)，則該長(zhǎng)方體的長(zhǎng)、寬、高相等，而對(duì)于任意的長(zhǎng)方體而言其長(zhǎng)、寬、高未必相等；對(duì)于④，以四面體的棱為一長(zhǎng)方體的側(cè)面的對(duì)角線構(gòu)造長(zhǎng)方體，該長(zhǎng)方體的體對(duì)角線的交點(diǎn)到該四面體的各頂點(diǎn)的距離相等；顯然該四面體的內(nèi)切球的球心到其各面的距離相等，故可判斷．
解答：對(duì)于①，容易得知，過三角形的內(nèi)心且垂直于該三角形所在平面的直線上任意一點(diǎn)到該三角形的各邊的距離都相等，因此①是真命題．
對(duì)于②，假設(shè)存在點(diǎn)到長(zhǎng)方形的各邊的距離相等，則該點(diǎn)到四個(gè)頂點(diǎn)的距離相等，該點(diǎn)必在過這個(gè)長(zhǎng)方形的中心且與這個(gè)長(zhǎng)方形所在的平面垂直的直線上，由此可知該長(zhǎng)方形的長(zhǎng)、寬相等，而對(duì)于任意的長(zhǎng)方形而言其長(zhǎng)、寬未必相等，因此②是假命題．
對(duì)于③，長(zhǎng)方體的體對(duì)角線的交點(diǎn)到各頂點(diǎn)的距離相等，若存在到長(zhǎng)方體的各個(gè)面距離相等的點(diǎn)，則該長(zhǎng)方體的長(zhǎng)、寬、高相等，而對(duì)于任意的長(zhǎng)方體而言其長(zhǎng)、寬、高未必相等，因此③是假命題．
對(duì)于④，以四面體的棱為一長(zhǎng)方體的側(cè)面的對(duì)角線構(gòu)造長(zhǎng)方體，可知該長(zhǎng)方體的體對(duì)角線的交點(diǎn)到該四面體的各頂點(diǎn)的距離相等；顯然該四面體的內(nèi)切球的球心到其各面的距離相等，因此④是真命題．
綜上所述，其中真命題的序號(hào)是①④
故答案為：①④
點(diǎn)評(píng)：本題以命題為載體，考查命題的真假判斷，解題時(shí)需要結(jié)合具體的幾何體，充分利用幾何體的性質(zhì)一一判斷．
在定義域內(nèi)是連續(xù)函數(shù)，數(shù)列{an}通項(xiàng)公式為an=
，則數(shù)列{an}的所有項(xiàng)之和為1．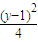
=1有唯一公共點(diǎn)的直線有且只有兩條．
，
，若函數(shù)f（x）=
在區(qū)間[-1，1]上是增函數(shù)，則實(shí)數(shù)t的取值范圍是（5，+∞）；