(-∞,-3]∪[3,+∞)

2或-8
分析:(A)由題意可得,|x+1|+|x-2|的最小值等于3,|a|≥3,由此求得 a的值.
(B)根據半圓的三等分點,得到三個弧對應的角度是60°,根據直徑所對的圓周角是直角得到直角三角形的有關長度,做出要求的線段的長度.
(C)把極坐標方程化為直角坐標方程的方法,根據直線和圓相切,利用點到直線的距離公式求出圓心到直線的距離等于半徑,從而求得a的值.
解答:(A)由于關于x的不等式|a|≥|x+1|+|x-2|存在實數解,而|x+1|+|x-2|表示數軸上的x對應點到-1和2對應點的距離之和,其最小值等于3,
∴|a|≥3,解得 a≥3,或 a≤-3,
故答案為 (-∞,-3]∪[3,+∞).
(B)∵A,E是半圓周上的兩個三等分點,∴弧EC是一個60°的弧,∴∠EBC=30°,則CE=2,連接BA,則BA=2,
∴在含有30°角的直角三角形中,BD=1,DT=

,AD=

,∴AF=

,
故答案為

.
(C)∵圓ρ=2cosθ 即ρ
2=2ρcosθ,即(x-1)
2+y
2=1,表示以(1,0)為圓心,半徑等于1的圓.
直線 3ρcosθ+4ρsinθ+a=0 即3x+4y+a=0,直線和圓相切,∴
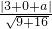
=1,解得a=2或-8,
故答案為:2或-8.
點評:本題主要考查絕對值不等式的解法,與圓有關的比例線段,考查圓周角定理,把極坐標方程化為直角坐標方程的方法,點到直線的距離公式的應用,直線和圓的位置關系,
屬于中檔題.

 (A)(不等式選做題)
(A)(不等式選做題) 2或-8
2或-8 ,AD=
,AD= ,∴AF=
,∴AF= ,
, .
.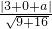 =1,解得a=2或-8,
=1,解得a=2或-8,

 閱讀快車系列答案
閱讀快車系列答案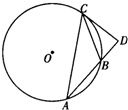 A.(不等式選做題)
A.(不等式選做題)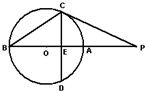 A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為
A.(不等式選做題)不等式|3x-6|-|x-4|>2x的解集為
 (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分) 選做題:(考生注意:請在下列三題中任選一題作答,如果多做,則按所做第一題評分)
選做題:(考生注意:請在下列三題中任選一題作答,如果多做,則按所做第一題評分)