
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的值域;
的值域;
(2)試問:函數(shù)![]() 的圖象上是否存在關(guān)于坐標原點對稱的點,若存在,求出這些點的坐標;若不存在,說明理由;
的圖象上是否存在關(guān)于坐標原點對稱的點,若存在,求出這些點的坐標;若不存在,說明理由;
(3)若方程![]() 的三個實數(shù)根
的三個實數(shù)根![]() 、
、![]() 、
、![]() 滿足:
滿足:![]() <
<![]() <
<![]() ,且
,且![]() ,求實數(shù)a的值.
,求實數(shù)a的值.
【答案】(1)![]() ;(2)存在,分別是
;(2)存在,分別是![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)分別求出函數(shù)在每段上的值域,最后求出整個函數(shù)的值域即可.
(2)假設(shè)存在這樣的點,不妨設(shè)![]() ,可求它的關(guān)于原點的對稱點坐標,再代入函數(shù)解析式中,能求出
,可求它的關(guān)于原點的對稱點坐標,再代入函數(shù)解析式中,能求出![]() 說明存在性,求不出
說明存在性,求不出![]() 則說明不存在這樣的點;
則說明不存在這樣的點;
(3)判斷![]() 之間的大小關(guān)系,然后分類化簡方程,求出三個實數(shù)根
之間的大小關(guān)系,然后分類化簡方程,求出三個實數(shù)根![]() 、
、![]() 、
、![]() ,再根據(jù)
,再根據(jù)![]() ,求出實數(shù)a的值.
,求出實數(shù)a的值.
(1)當![]() 時,
時, ![]()
當![]() 時,
時, ![]() ,因此函數(shù)的值域為
,因此函數(shù)的值域為![]() ;
;
(2) 假設(shè)存在這樣的點,不妨設(shè)![]() ,它關(guān)于原點的對稱點坐標為:
,它關(guān)于原點的對稱點坐標為:
![]() ,由題意可知它也在函數(shù)圖象上,因此有
,由題意可知它也在函數(shù)圖象上,因此有
![]() (舍去),
(舍去),
因此存在這樣兩個點,坐標分別為![]() 和
和![]() ;
;
(3)由(1)可知:當![]() 時,
時, ![]() ,顯然此時,
,顯然此時, ![]() ,
,
當![]() 時,若
時,若![]() 時,解得
時,解得![]() ,若
,若![]() 時,解得
時,解得
![]() .
.
因此當![]() 時,
時, ![]() ,此時方程化簡為:
,此時方程化簡為:![]()
解得![]() ,因此有
,因此有![]() .
.
當![]() 時,
時, ![]() ,此時方程化簡為:
,此時方程化簡為:![]() ,解得
,解得
![]() ,要想方程有三個不同的根,則必有
,要想方程有三個不同的根,則必有![]() ,此時
,此時
![]() 成立,因此有
成立,因此有![]() ,
,
又因為![]() ,
,
所以![]() ,解得
,解得![]() (舍去),
(舍去), ![]() .
.
![]() ,因此
,因此![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)討論函數(shù)![]() 極值點的個數(shù),并說明理由;
極值點的個數(shù),并說明理由;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的最大整數(shù)值.
的最大整數(shù)值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 平面
平面![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)過點![]() 作一平行于平面
作一平行于平面![]() 的截面,畫出該截面,說明理由,并求夾在該截面與平面
的截面,畫出該截面,說明理由,并求夾在該截面與平面![]() 之間的幾何體的體積.
之間的幾何體的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且
,且![]() ,圓
,圓![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() ,
,![]() 面積最大值為
面積最大值為![]() .
.
(1)求圓![]() 與橢圓
與橢圓![]() 的方程;
的方程;
(2)圓![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了調(diào)查某生產(chǎn)線上質(zhì)量監(jiān)督員甲是否在現(xiàn)場對產(chǎn)品質(zhì)量好壞有無影響,現(xiàn)統(tǒng)計數(shù)據(jù)如下:質(zhì)量監(jiān)督員甲在現(xiàn)場時,1 000件產(chǎn)品中合格品有990件,次品有10件,甲不在現(xiàn)場時,500件產(chǎn)品中有合格品490件,次品有10件.
(1)補充下面列聯(lián)表,并初步判斷甲在不在現(xiàn)場與產(chǎn)品質(zhì)量是否有關(guān):
合格品數(shù)/件 | 次品數(shù)/件 | 總數(shù)/件 | |
甲在現(xiàn)場 | 990 | ||
甲不在現(xiàn)場 | 10 | ||
總數(shù)/件 |
(2)用獨立性檢驗的方法判斷能否在犯錯誤的概率不超過0.15的前提下認為“甲在不在現(xiàn)場與產(chǎn)品質(zhì)量有關(guān)”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
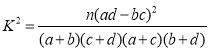
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 上的點均在曲線
上的點均在曲線![]() 外,且對
外,且對![]() 上任意一點
上任意一點![]() ,
,![]() 到直線
到直線![]() 的距離等于該點與曲線
的距離等于該點與曲線![]() 上點的距離的最小值.
上點的距離的最小值.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,過點
,過點![]() 的直線與曲線
的直線與曲線![]() 交于另一點
交于另一點![]() ,且直線
,且直線![]() 過點
過點![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com