
【題目】如圖,在幾何體![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
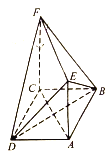
(1)證明:平面![]() 平面
平面![]() .
.
(2)若二面角![]() 是直二面角,求
是直二面角,求![]() 與平面
與平面![]() 所成角的正切值。
所成角的正切值。
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)利用面面垂直的判定定理證明即可; (2)利用二面角![]() 是直二面角,求出菱形
是直二面角,求出菱形![]() 的邊長,再求出
的邊長,再求出![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
試題解析:(1)證明:∵四邊形![]() 是菱形,∴
是菱形,∴![]()
∵![]() 平面
平面![]() ∴
∴![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() ∴平面
∴平面![]() ⊥平面
⊥平面![]()
(2)(向量)解:以點![]() 為原點,
為原點, ![]() 方向為
方向為![]() 軸,
軸, ![]() 方向為
方向為![]() 軸,
軸, ![]() 方向為
方向為![]() 軸建立空間直角坐標系,如圖。做
軸建立空間直角坐標系,如圖。做![]() 的中點
的中點![]() ,連接
,連接![]() ,因為
,因為![]() 平行且等于
平行且等于![]() ,
, ![]() .
.
所以四邊形![]() 為平行四邊形,
為平行四邊形,
因為在![]() 中,
中, ![]() ,所以
,所以![]() ,所以
,所以![]()
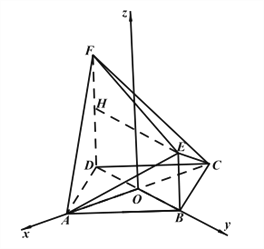
設![]() 長為
長為![]() ,則各點坐標為
,則各點坐標為
![]() ;
; ![]() ;
; ![]() ;
; ![]()
所以![]() ;
; ![]() ;
; ![]()
設![]() 為面
為面![]() 的法向量;
的法向量; ![]() 為面
為面![]() 的法向量。
的法向量。
所以![]() ;
; ![]()
得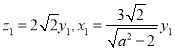
令![]() 得
得![]()
同理得![]()
因為二面角![]() 是直二面角,所以
是直二面角,所以![]()
得![]()
由題可得: ![]() 為
為![]() 與平面
與平面![]() 所夾角
所夾角
因為![]()
所以![]()
(幾何)
∵四邊形![]() 是菱形,∴
是菱形,∴![]()
∴![]() ,∴
,∴![]()
過![]() 作
作![]() ,連接
,連接![]() ,則
,則![]() 為
為![]() 二面角的平面角
二面角的平面角
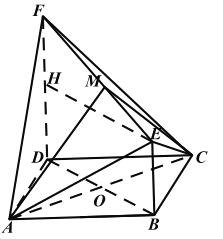
設菱形的邊長為![]()
∵![]() ,
, ![]() ,∴
,∴ ![]()
在![]() 中,
中, ![]() ,∴
,∴![]()
∵![]() 二面角為直角,∴
二面角為直角,∴![]() 為直角
為直角
∴![]()
在![]() 中,
中, ![]() ,設
,設![]() ,則
,則![]()
![]()
![]() ∴
∴![]()
![]() 與平面
與平面![]() 所成角為
所成角為![]()
∴![]()


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,過
,過![]() 、
、![]() 、
、![]() 三點的圓
三點的圓![]() 的圓心坐標為
的圓心坐標為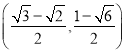 .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)若直線![]() (
(![]() 為常數,
為常數, ![]() )與橢圓
)與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 和
和![]() .
.
(ⅰ)當直線![]() 過
過![]() ,且
,且![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(ⅱ)當坐標原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,且
,且![]() 面積為
面積為![]() 時,求直線
時,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】觀察圖中各正方形圖案,每條邊上有an個圓點,第an個圖案中圓點的個數是an,按此規律推斷出所有圓點總和Sn與n的關系式為( )
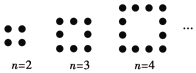
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
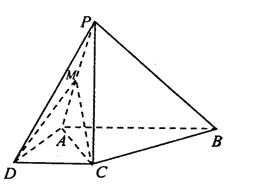
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 的中點,且過
的中點,且過![]() 三點的平面與線段
三點的平面與線段![]() 交于點
交于點![]() ,確定點
,確定點![]() 的位置,說明理由;并求三棱錐
的位置,說明理由;并求三棱錐![]() 的高.
的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
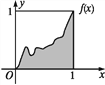
【題目】設函數y=f(x)在區間[0,1]上的圖象是連續不斷的一條曲線,且恒有0≤f(x)≤1,可以用隨機模擬方法近似計算由曲線y=f(x)及直線x=0,x=1,y=0所圍成部分的面積S.先產生兩組(每組N個)0~1區間上的均勻隨機數x1,x2,…,xN和y1,y2,…,yN,由此得到N個點(xi,yi)(i=1,2,…,N).再數出其中滿足yi≤f(xi)(i=1,2,…,N)的點數N1,那么由隨機模擬方法可得S的近似值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,M、N、P分別是正方體ABCD-A1B1C1D1的棱AB、BC、DD1上的點.
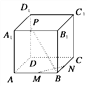
(1)若![]() ,求證:無論點P在DD1上如何移動,總有BP⊥MN;
,求證:無論點P在DD1上如何移動,總有BP⊥MN;
(2)棱DD1上是否存在這樣的點P,使得平面APC1⊥平面ACC1?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系xOy中,圓C的參數方程為![]() (θ為參數),直線l經過定點P(2,3),傾斜角為
(θ為參數),直線l經過定點P(2,3),傾斜角為![]() .
.
(Ⅰ)寫出直線l的參數方程和圓C的標準方程;
(Ⅱ)設直線l與圓C相交于A,B兩點,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產的某種產品被檢測出其中一項質量指標存在問題.該企業為了檢查生產該產品的甲,乙兩條流水線的生產情況,隨機地從這兩條流水線上生產的大量產品中各抽取50件產品作為樣本,測出它們的這一項質量指標值.若該項質量指標值落在![]() 內,則為合格品,否則為不合格品.表1是甲流水線樣本的頻數分布表,圖1是乙流水線樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.表1是甲流水線樣本的頻數分布表,圖1是乙流水線樣本的頻率分布直方圖.
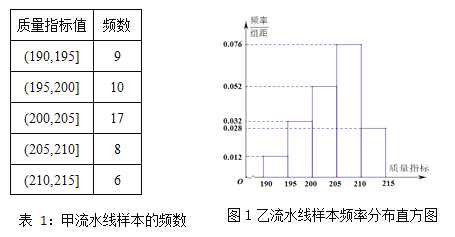
(1)根據圖,1估計乙流水線生產產品該質量指標值的中位數;
(2)若將頻率視為概率,某個月內甲,乙兩條流水線均生產了5000件產品,則甲,乙兩條流水線分別生產出不合格品約多少件?
(3)根據已知條件完成下面![]() 列聯表,并回答是否有85%的把握認為“該企業生產的這種產品的質量指標值與甲,乙兩條流水線的選擇有關”?
列聯表,并回答是否有85%的把握認為“該企業生產的這種產品的質量指標值與甲,乙兩條流水線的選擇有關”?
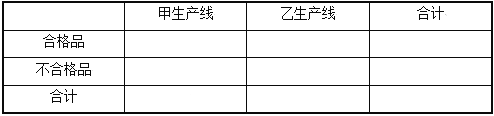
附: ![]() (其中
(其中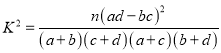 為樣本容量)
為樣本容量)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標平面內,以坐標原點O為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程是
軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程是![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com